- ... matemático

- A partir da década de 50
o esforço na direção de uma construção mais rigorosa da teoria
culminou no que ficou conhecido como teoria axiomática
[1].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
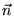

- Os
sítios na rede são indexados pelos vetores
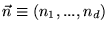 ,
onde cada
,
onde cada 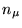 é um número inteiro
que varia de 1 a N.
é um número inteiro
que varia de 1 a N.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
analiticamente
- A dedução dos resultados apresentados neste
capítulo está detalhada na referência [9]. No âmbito desta
tese nos restringimos apenas a reportar os resultados básicos
necessários para cálculos futuros.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... rede
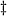
- Por simplicidade de apresentação estamos
desconsiderando a questão de N ser par ou ímpar. Cada caso pode ser
considerado em detalhe, levando aos mesmos resultados finais no limite
do contínuo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
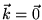

- Podemos entender as fatorações acima em
termos dos diagramas de Feymann. Considere, por exemplo, n=2 e
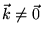 .
Neste caso existem quatro linhas externas para
serem ligadas entre si, duas com momento
.
Neste caso existem quatro linhas externas para
serem ligadas entre si, duas com momento 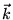 e duas com momento
e duas com momento
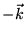 (pois para o campo escalar real vale que
(pois para o campo escalar real vale que
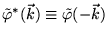 ). Para
haver a conservação do momento total as linhas com momento
). Para
haver a conservação do momento total as linhas com momento 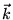 só podem ser ligadas às linhas com momento
só podem ser ligadas às linhas com momento 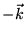 ;
ou seja, duas
possibilidades de ligação. Isso pode ser facilmente generalizado para
o caso n qualquer, levando aos resultados mencionados. Já para
;
ou seja, duas
possibilidades de ligação. Isso pode ser facilmente generalizado para
o caso n qualquer, levando aos resultados mencionados. Já para
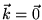 e n=2 existem três possibilidades de ligação, já
que o momento é sempre conservado.
e n=2 existem três possibilidades de ligação, já
que o momento é sempre conservado.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Euclidiano

- O fato de
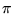 diferir de
diferir de
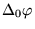 por um fator imaginário condiz com a sua
definição. Para perceber isso basta lembrarmos que classicamente ele
está associado a uma derivada temporal e é justamente sobre esta
componente que aplicamos a rotação de Wick para irmos do espaço de
Euclides para o de Minkowski.
por um fator imaginário condiz com a sua
definição. Para perceber isso basta lembrarmos que classicamente ele
está associado a uma derivada temporal e é justamente sobre esta
componente que aplicamos a rotação de Wick para irmos do espaço de
Euclides para o de Minkowski.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
variáveis
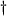
- Este problema não aparecia na teoria
clássica onde por construção
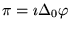 no espaço
Euclidiano. Aqui estamos fazendo uma generalização, assumindo que
no espaço
Euclidiano. Aqui estamos fazendo uma generalização, assumindo que
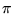 pode ser uma variável independente de
pode ser uma variável independente de
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
a
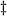
- Neste momento ainda existe um abuso de linguagem ao
associarmos os ensembles a partículas, pois ainda não sabemos
muito bem o que são estas ``partículas'', uma vez que não
identificamos a sua massa nem a sua energia.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ação

- Na
quantização do campo escalar no contínuo temos que o operador número
de partículas está relacionado com a Hamiltoniana do sistema ou seja
e
onde
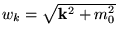 e sendo
e sendo
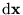 e
e
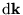 integrais definidas numa
superfície espacial. Aqui, como estamos no espaço Euclidiano, a coisa
mais natural a se fazer é olhar para as integrais definidas no
espaço-tempo quadridimensional,
integrais definidas numa
superfície espacial. Aqui, como estamos no espaço Euclidiano, a coisa
mais natural a se fazer é olhar para as integrais definidas no
espaço-tempo quadridimensional,
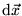 e
e
 .
Isso é, de certa forma, uma
generalização do caso tridimensional porque neste modelo existe
invariança translacional e estamos utilizando condições periódicas de
contorno.
.
Isso é, de certa forma, uma
generalização do caso tridimensional porque neste modelo existe
invariança translacional e estamos utilizando condições periódicas de
contorno.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
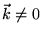
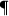
- Para
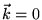 temos
temos
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... como

- Aqui estamos fazendo na rede a subtração do
termo divergente que no contínuo é feita através da ordenação de Wick
do operador
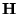 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
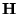
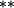
- A Hamiltoniana dimensional
deve ter a mesma unidade da energia, ou seja, unidade de massa ou o
inverso de comprimento. Por outro lado, lembrando que
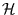 contém uma derivada temporal, pois está relacionado com
contém uma derivada temporal, pois está relacionado com
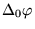 ,
escrevemos
,
escrevemos 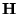 ', a Hamiltoniana dimensional, como
', a Hamiltoniana dimensional, como
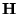 '
'
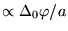 ,
que no limite do contínuo
será proporcional a
,
que no limite do contínuo
será proporcional a
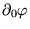 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
delas.

- Desta maneira estamos efetuando 100.000.000 mudanças
nas configurações dos campos para cada um dos observáveis, o que
diminui consideravelmente os seus respectivos erros. Por outro lado
esta estatítistica só é possível em redes pequenas com os recursos
computacionais disponíveis para o projeto. Na análise do limite do
contínuo somos, portanto, obrigados a diminuir estes valores.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....
- Lembremo-nos de que o
comportamento crítico só existe no limite do contínuo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....
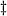
- Como já dissemos,
a linha crítica só faz sentido no limite do contínuo e nesta situação
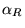 deve ser nulo para que
deve ser nulo para que
 seja
finito.
seja
finito.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
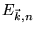

- Nos
gráficos apresentados a seguir estaremos considerando por simplicidade
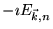 ao invés de
ao invés de 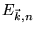 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... grandes
- Como já discutimos anteriormente,
esta parte da análise é apenas qualitativa.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ordem

- Aqui estamos, por simplicidade
considerando
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![]() e sendo
e sendo
![]() e
e
![]() integrais definidas numa
superfície espacial. Aqui, como estamos no espaço Euclidiano, a coisa
mais natural a se fazer é olhar para as integrais definidas no
espaço-tempo quadridimensional,
integrais definidas numa
superfície espacial. Aqui, como estamos no espaço Euclidiano, a coisa
mais natural a se fazer é olhar para as integrais definidas no
espaço-tempo quadridimensional,
![]() e
e
![]() .
Isso é, de certa forma, uma
generalização do caso tridimensional porque neste modelo existe
invariança translacional e estamos utilizando condições periódicas de
contorno.
.
Isso é, de certa forma, uma
generalização do caso tridimensional porque neste modelo existe
invariança translacional e estamos utilizando condições periódicas de
contorno.