![\begin{displaymath}
{\cal{H}}[\pi]=-\frac{\imath\pi^2}{2} - \frac{\imath}{2} \sum_i(\Delta_i \varphi)^2 -
\frac{\imath \alpha_0}{2} \varphi^2
\end{displaymath}](img126.png)
![\begin{displaymath}
{\cal{H}}[\pi]=-\frac{\imath\pi^2}{2} - \frac{\imath}{2} \sum_i(\Delta_i \varphi)^2 -
\frac{\imath \alpha_0}{2} \varphi^2
\end{displaymath}](img126.png)
e de
![]() em (4.2),
em (4.2),
![\begin{eqnarray*}
{\cal{L}}[\pi, \varphi] &=& -\imath \pi \Delta_0 \varphi +\ima...
...}{2}
\sum_i (\Delta_i \varphi)^2 + \frac{\alpha_0}{2} \varphi^2,
\end{eqnarray*}](img128.png)
vamos inicialmente calcular a média da ação![]() nos estados de vácuo e de n partículas. Usando a
definição onde
nos estados de vácuo e de n partículas. Usando a
definição onde
![]() (4.5) temos, para o
estado de vácuo,
(4.5) temos, para o
estado de vácuo,
![\begin{eqnarray*}
\left\langle S\right\rangle_0^{\pi \not= \imath\Delta_0 \varph...
... \pi] e^{-\frac{1}{2} \sum_s (\pi - \imath \Delta_0 \varphi)²}},
\end{eqnarray*}](img138.png)
onde completamos quadrados na ação. Novamente, em analogia
ao caso de um observável qualquer ![]() ,
temos que
,
temos que
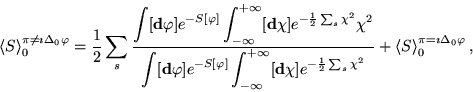
onde
![]() e o superscrito que
aparece no segundo valor esperado indica que ele está sendo tomado no
ensemble onde
e o superscrito que
aparece no segundo valor esperado indica que ele está sendo tomado no
ensemble onde
![]() .
.
Agora usando alguns resultados já conhecidos de integração Gaussiana e integrais de resíduos, chegamos a
e repetindo os cálculos para o estado de n partículas,
Este resultado nos mostra que os dois ensembles diferem por uma
quantidade divergente porém constante no limite do
contínuo. Podemos portanto calcular somente os observáveis no ensemble onde
![]() .
Para isso vamos para o espaço
de momentos onde a ação é diagonalizada, podendo ser escrita como
(3.7),
.
Para isso vamos para o espaço
de momentos onde a ação é diagonalizada, podendo ser escrita como
(3.7),
![\begin{displaymath}
S[\tilde{\varphi}]=\frac{N_L^{d-1}N_T}{2}
\sum_{\vec{k}}\lef...
...^2
+\alpha_0\right]{\vert \tilde{\varphi_{\vec{k}}} \vert}^2.
\end{displaymath}](img143.png)
onde
![$\rho^2 \equiv \sum_{\mu} \rho_{\mu}^2 \equiv
\sum_{\mu}\left[ 2\sin{\frac{\pi k_{\mu}}{N_{\mu}}}\right]^2$](img144.png) .
A média
da ação é portando obtida, lembrando (3.4), com o uso de
.
A média
da ação é portando obtida, lembrando (3.4), com o uso de
chegando-se portanto ao resultado
Para o estado de n partículas obtemos analogamente
onde usamos o seguinte resultado para
![]() e l,m quaisquer:
e l,m quaisquer:
Podemos portanto definir na rede um observável número de partículas
![]() como
como![]()
de tal forma que
e assim por diante. Vale salientar que para o campo escalar real e para os ensembles definidos por (4.6) não existe como diferenciar partículas com quadri-momentos iguais em módulo e com direções contrárias, uma vez que elas podem ser consideradas como partículas de cargas contrárias andando com o mesmo momento. O que medimos aqui são partículas ``neutras''que englobam partículas com cargas ``positivas'' e ``negativas''. Temos aqui o primeiro indício da necessidade física de que o modelo contenha o conceito de carga.