Cálculo da Energia

Calculando $\left\langle{\bf H} \right\rangle$ no estado de vácuo a partir da definição (4.2) e da equação (4.5) temos

$$\begin{eqnarray*} \left\langle {\bf H}\right\rangle_0^{\pi \not= \imath \Delta_0... ... \infty}^{+ \infty} [{\bf d} \chi] e^{-\sum_s \frac{\chi²}{2}}}, \end{eqnarray*}$$

onde $\chi \equiv \pi - \imath \Delta_0 \varphi$. Reescrevendo a expressão acima com ${\bf H}$ expresso em termos de $\chi$ e $\Delta_0 \varphi$, e considerando que, neste caso

$$\int_{-\infty}^{+\infty} [{\bf d} \chi] \chi e^{-\frac{1}{2}\sum_s \chi^2} = 0$$

por simetria, chegamos a

$$\begin{eqnarray*} \left\langle{\bf H}\right\rangle_0^{\pi \not= \imath \Delta_0 ... ... \varphi^2 \right]}{\displaystyle \int [{\bf d} \varphi]e^{-S}}. \end{eqnarray*}$$

Assim obtemos facilmente que

$$\begin{eqnarray*} \left\langle{\bf H}\right\rangle_0^{\pi \not= \imath \Delta_0 ... ...alpha_0 \varphi^2 \right\rangle_0^{\pi=\imath \Delta_0 \varphi}, \end{eqnarray*}$$

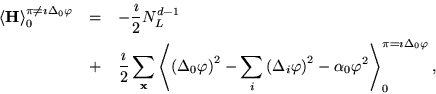
resultado análogo ao obtido para o operador número de partículas. Em termos da energia do sistema temos

$$\begin{eqnarray*} E_0 &\equiv& E_0^{\pi\not=\imath \Delta_0 \varphi} = \frac{1}{... ...^2 -\alpha_0 \varphi^2 \right\rangle_0^{\pi = \Delta_0 \varphi}. \end{eqnarray*}$$

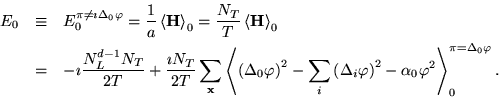
onde o fator 1/a relaciona a grandeza dimensional E com a grandeza adimensional ${\bf H}$.

O próximo passo consiste em estudar melhor a equação acima, indo para o espaço de momentos, onde ${\bf H}$, assim como S, é diagonalizado. Para executar esta operação precisamos antes utilizar a invariança translacional na direção temporal do sistema, para completar a soma na parte espacial. Assim temos

$$\begin{eqnarray*} E_0 &=& -\imath \frac{N_L^{d-1}N_T}{2T} + \imath\frac{N_T}{2T}... ...ight] }{\displaystyle \int[{\bf {d}} \varphi ] e^{-S[\varphi]}}. \end{eqnarray*}$$

Agora podemos aplicar as transformadas finitas de Fourier (3.6) e utilizando o valor de $\langle{\vert \tilde{\varphi}_{\vec{k}} \vert }^2 \rangle$ dado em (3.4), chegamos a

$$E_0 = - \frac{\imath}{T} \sum_{\vec{k}} \frac{{\mbox{\boldmath$\mathfrak{\rho}$}}^2 + \alpha_0}{\rho^2 + \alpha_0}.$$ (4.12)

onde ${\mbox{\boldmath$\mathfrak{\rho}$}}^2 \equiv \sum_i \rho_i^2 \equiv \sum_i\left[ 2\sin{\frac{\pi k_i}{N}}\right]^2$ é definido como a soma somente sobre as componentes espaciais, de forma que $\rho^2 = {\mbox{\boldmath$\mathfrak{\rho}$}}^2 + \rho_0^2$. Repetindo os cálculos para o ensemble de uma partícula com momento $\vec{k}$ chegamos a

$$\begin{eqnarray*} \langle{\bf H}\rangle_{\vec{k},1}^{\pi \not= \imath \Delta_0 \... ...hi ] {\vert \tilde{\varphi}_{\vec{k}} \vert}^2 e^{-S[\varphi]}}. \end{eqnarray*}$$

A energia é, portanto, dada por

$$\begin{eqnarray*} E_{\vec{k},1}&=&-\imath \frac{{N_L}^{d-1} N_T}{2T}\\ &+&\imat... ...hi ] {\vert \tilde{\varphi_{\vec{k}}} \vert}^2 e^{-S[\varphi]}}. \end{eqnarray*}$$

Utilizando novamente a invariança translacional, a relação de fatoração

$$\langle{\vert \tilde{\varphi _{\vec{k}}} \vert}^{2n}\rangle=n!\langle{\vert \tilde{\varphi _{\vec{k}}} \vert}^2\rangle^n$$

e o resultado

$$\langle{\vert \tilde{\varphi}_{\vec{k}} \vert}^2\rangle=\frac{1}{N_L^{d-1}N_T(\rho^2 + \alpha_0)},$$

chegamos a

$$E_{\vec{k},1} = -\frac{\imath}{T} \sum_{\vec{k}} \frac{{\mbo... ...{\rho}$}}^2 + \alpha_0}{\rho^2 + \alpha_0} \right)_{\vec{k}}.$$ (4.13)

Se compararmos a equação acima com (4.12) podemos definir uma grandeza $\Delta E_{\vec{k}}$ como

$$\Delta E_{\vec{k}} \equiv \Delta E_{\vec{k},1} \equiv E_{\ve... ...k{\rho}$}}^2 + \alpha_o}{\rho^2 + \alpha_0} \right)_{\vec{k}}.$$ (4.14)

Para o estado de n partículas de momento $\vec{k}$ os cálculos são análogos aos já feitos e chegamos facilmente a

$$\Delta E_{\vec{k},n} \equiv E_{\vec{k},n} - E_0 = -\imath \f... ...k{\rho}$}}^2 + \alpha_o}{\rho^2 + \alpha_0} \right)_{\vec{k}}.$$

Este é um resultado interessante: para uma rede finita e um momento $\vec{k}$ bem definido existe uma quantidade fixa $\Delta E_{\vec{k}}$ que depende somente dos valores de $\alpha_0$ e $\vec{k}$ e que exibe a propriedade de comportar-se com um ``pacote de energia''. Apesar de não termos definido muito bem o que significa fisicamente a quantidade $\alpha_0$ porque ainda não definimos o que entendemos por partícula neste formalismo, esta quantidade já aparece sem que precisemos tomar o limite do contínuo ou, no mínimo, o limite de tempo infinito. Em outras palavras, na rede finita já encontramos um espectro discreto de energia com espaçamento fixo e constante dado por $\Delta E_{\vec{k}}$. Nas seções seguintes discutiremos melhor este resultado.