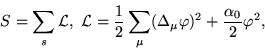
Utilizando a ação da teoria livre na rede Euclidiana, temos
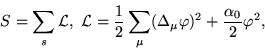
onde tanto S quanto ![]() são adimensionais, sendo
são adimensionais, sendo ![]() a densidade
Lagrangiana adimensional. A versão canônica da teoria clássica define
um momento conjugado ao campo
a densidade
Lagrangiana adimensional. A versão canônica da teoria clássica define
um momento conjugado ao campo ![]() como
como
onde o fator complexo ![]() é adicionado por estarmos
trabalhando no espaço-tempo Euclidiano
é adicionado por estarmos
trabalhando no espaço-tempo Euclidiano![]() e o índice s expressa o fato que
e o índice s expressa o fato que
![]() é uma variável de sítio associada ao link 0 que sai de cada
sítio, relacionado com a direção temporal. Da definição acima surge a
necessidade de separar o índice temporal dos índices espaciais da
rede. Assim, de agora em diante as somas d-dimensionais serão
expressas por
é uma variável de sítio associada ao link 0 que sai de cada
sítio, relacionado com a direção temporal. Da definição acima surge a
necessidade de separar o índice temporal dos índices espaciais da
rede. Assim, de agora em diante as somas d-dimensionais serão
expressas por ![]() ou
ou ![]() ,
as somas somente numa
superfície espacial por
,
as somas somente numa
superfície espacial por
![]() ou
ou ![]() e as variáveis
temporais por 0 ou t. A rede terá NL sítios nas direções
espaciais e NT sítios na direção temporal. Em geral estes dois
números serão iguais, mas fica aberta a possibilidade de que sejam
diferentes quando isto for necessário para futuras discussões. As
direções espaciais terão comprimento L e a direção temporal terá
comprimento T. O espaçamento da rede será sempre a, de forma que
e as variáveis
temporais por 0 ou t. A rede terá NL sítios nas direções
espaciais e NT sítios na direção temporal. Em geral estes dois
números serão iguais, mas fica aberta a possibilidade de que sejam
diferentes quando isto for necessário para futuras discussões. As
direções espaciais terão comprimento L e a direção temporal terá
comprimento T. O espaçamento da rede será sempre a, de forma que
Expressando a ação em termos desta notação temos que
e
Podemos agora definir uma densidade Hamiltoniana adimensional ![]() na rede de maneira que os resultados sejam compatíveis com os
resultados no limite do contínuo e as integrais convirjam no espaço
Euclidiano. Note que a teoria quântica de campos usual é desenvolvida
no espaço de Minkowski, onde as equações de movimento são invariantes
por transformações de Lorentz. Porém mesmo lá, para que as integrais
funcionais convirjam, é necessário fazer uma rotação de Wick na
componente temporal, utilizando o espaço Euclidiano somente para
resolver as integrais e depois retornando ao espaço de Minkowski. Como
na rede trabalhamos com o espaço Euclidiano todo o tempo, basta
descobrir quais definições de S e
na rede de maneira que os resultados sejam compatíveis com os
resultados no limite do contínuo e as integrais convirjam no espaço
Euclidiano. Note que a teoria quântica de campos usual é desenvolvida
no espaço de Minkowski, onde as equações de movimento são invariantes
por transformações de Lorentz. Porém mesmo lá, para que as integrais
funcionais convirjam, é necessário fazer uma rotação de Wick na
componente temporal, utilizando o espaço Euclidiano somente para
resolver as integrais e depois retornando ao espaço de Minkowski. Como
na rede trabalhamos com o espaço Euclidiano todo o tempo, basta
descobrir quais definições de S e ![]() fazem sentido
físico. Vamos manter uma definição compatível com o caso clássico e
analisar posteriormente as consequências para a teoria
quântica. Assim,
fazem sentido
físico. Vamos manter uma definição compatível com o caso clássico e
analisar posteriormente as consequências para a teoria
quântica. Assim, ![]() será definido classicamente na rede como
será definido classicamente na rede como
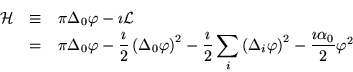
ou, em termos de ![]() e
e ![]() somente,
somente,
Podemos ainda escrever ![]() e
e ![]() ,
a Lagrangiana e a
Hamiltoniana do sistema, como sendo as somas espaciais sobre as
respectivas densidades. Assim,
,
a Lagrangiana e a
Hamiltoniana do sistema, como sendo as somas espaciais sobre as
respectivas densidades. Assim,
| = | |||
| = | ![$\displaystyle -\frac{\imath}{2}\sum_{\mathbf{x}}\left[ \pi^2 +\sum_i\left(
\Delta_i \varphi \right)^2 + \alpha_0 \varphi^2 \right]$](img99.png) |
(4.2) |
e
![\begin{eqnarray*}
{\bf L}[\Delta_0 \varphi] &=& \sum_{\mathbf{x}} {\cal L}[\Delt...
...^2) + \sum_i (\Delta_i
\varphi)^2 + \alpha_0 \varphi^2 \right].
\end{eqnarray*}](img100.png)
Para discutirmos a teoria quântica vamos utilizar a definição via integração funcional, onde o que temos são os observáveis da teoria expressos por
![\begin{displaymath}
\left\langle {\cal O}\right\rangle_N \equiv \frac{\displayst...
...\varphi] e^{-S}}{\displaystyle \int [{\bf d} \varphi] e^{-S}}.
\end{displaymath}](img36.png)
Neste ponto temos duas maneiras de continuar os cálculos, a primeira
delas considerando ![]() e
e
![]() como variáveis
independentes e a outra considerando-as como as mesmas
variáveis
como variáveis
independentes e a outra considerando-as como as mesmas
variáveis![]() . Vamos estudar detalhadamente cada uma delas.
. Vamos estudar detalhadamente cada uma delas.
No primeiro caso, os observáveis são definidos como
onde neste caso consideramos a seguinte generalização:
| = | 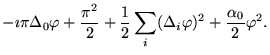 |
(4.4) |
Após alguns cálculos chegamos a
Precisamos agora calcular a integral
Efetuando a mudança de variáveis
![]() chegamos finalmente a
chegamos finalmente a
e para um observável que não dependa de ![]() temos, da
equação (4.5),
temos, da
equação (4.5),
![\begin{displaymath}
\left\langle {\cal O}\right\rangle = \frac{\displaystyle \in...
...rphi]}}{\displaystyle \int [{\bf d} \varphi] e^{-S[\varphi]}},
\end{displaymath}](img113.png)
onde
![]() .
Ou seja, para
.
Ou seja, para
![]() este formalismo é idêntico ao formalismo em que
este formalismo é idêntico ao formalismo em que
![]() .
.
No entanto, quando os observáveis dependem tanto de ![]() como de
como de
![]() este resultado já não é mais válido e precisamos voltar à
definição (4.5). Desta maneira pode-se demonstrar, por
exemplo, que
este resultado já não é mais válido e precisamos voltar à
definição (4.5). Desta maneira pode-se demonstrar, por
exemplo, que
![]() e que
e que
![]() .
Este resultado indica uma diferença conceitual
entre os campos clássico e quântico. Classicamente não existe
diferença entre as variáveis
.
Este resultado indica uma diferença conceitual
entre os campos clássico e quântico. Classicamente não existe
diferença entre as variáveis ![]() e
e
![]() .
Quanticamente porém somente os valores esperados de
.
Quanticamente porém somente os valores esperados de ![]() e
e
![]() são iguais.
são iguais.
De agora em diante, portanto, utilizaremos a definição geral dada por (4.3).
Precisamos agora mapear esta definição dos observáveis na rede nos valores esperados de observáveis em estados de partículas como é usual no caso do formalismo de operadores.
A idéia é associar o estado de vácuo a um particular ensemble do modelo, aquele que estivemos usando até agora,
![\begin{displaymath}
\vert\rangle \sim \frac{\displaystyle [{\bf d} \varphi] e^{-S[\varphi]}}{\displaystyle \int[{\bf d}
\varphi] e^{-S[\varphi]}}
\end{displaymath}](img118.png)
ou
![\begin{displaymath}
\vert\rangle \sim \frac{\displaystyle [{\bf d} \varphi][{\bf...
...tyle \int [{\bf d} \varphi][{\bf d} \pi]
e^{-S[\varphi,\pi]}},
\end{displaymath}](img119.png)
o estado de uma ``partícula'' de momento ![]() a
a![]()
![\begin{displaymath}
\vert{\vec{k}},1\rangle \sim \frac{\displaystyle [{\bf d}
\v...
...\varphi]\vert\tilde{\varphi}_{\vec{k}}\vert^2 e^{-S[\varphi]}}
\end{displaymath}](img121.png)
ou
![\begin{displaymath}
\vert{\vec{k}},1\rangle \sim \frac{\displaystyle [{\bf d} \v...
...\pi]\vert\tilde{\varphi}_{\vec{k}}\vert^2
e^{-S[\varphi,\pi]}}
\end{displaymath}](img122.png)
![\begin{displaymath}
\vert{\vec{k}},n\rangle \sim \frac{\displaystyle [{\bf d}
\v...
...rphi]\vert\tilde{\varphi}_{\vec{k}}\vert^{2n} e^{-S[\varphi]}}
\end{displaymath}](img123.png)
ou
Precisamos portanto analisar o que representam estes ensembles do ponto de vista da construção do espaço de Fock. Para isso vamos calcular neles os observáveis número de partículas e energia do sistema.