Utilizamos o campo escalar livre de uma única componente como
laboratório para calcular alguns observáveis da teoria
analiticamente![]() .
.
A ação deste modelo é definida na rede como
Esta teoria é interessante porque todas as integrais envolvidas são Gaussianas e, assim sendo, solúveis na rede. Pode-se demonstrar, por exemplo, que a função de dois pontos do modelo no espaço de momentos é expressa por
onde
![$\rho^2 \equiv \sum_{\mu} \rho_{\mu}^2 \equiv
\sum_{\mu}\left[ 2\sin{\frac{\pi k_{\mu}}{N}}\right]^2$](img42.png) são os
momentos adimensionais definidos na rede e
são os
momentos adimensionais definidos na rede e
![]() com ki variando de -N/2 a +N/2 são os modos
de Fourier da rede
com ki variando de -N/2 a +N/2 são os modos
de Fourier da rede![]() . Podemos ainda expressar estas funções no espaço de
configurações, simplesmente aplicando uma transformada finita inversa
de Fourier à expressão (3.4). Obtemos assim
. Podemos ainda expressar estas funções no espaço de
configurações, simplesmente aplicando uma transformada finita inversa
de Fourier à expressão (3.4). Obtemos assim
onde definimos a transformada finita de Fourier e sua inversa respectivamente como
e
Na linguagem da rede Euclidiana frequentemente usamos o termo função de correlação de dois pontos para representar os observáveis (3.4) e (3.5).
Além disso este modelo exibe uma propriedade interessante, a diagonalização da ação no espaço de momentos. Obtemos este resultado aplicando as transformadas finitas de Fourier (3.6) na ação definida por (3.3) e considerando as relações de ortogonalidade e completeza,
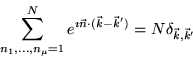
e
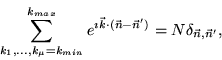
respectivamente, onde ![]() varia de 1 a d e kmin
e kmax representam os limites inferiores e superiores para os
momentos na rede. Chegamos
assim a
varia de 1 a d e kmin
e kmax representam os limites inferiores e superiores para os
momentos na rede. Chegamos
assim a
Outra propriedade interessante é a fatoração das funções de
correlação. Este resultado é uma consequência direta de
(3.4), (3.7) e da definição (3.2). Derivando
os dois lados de (3.4) com relação a
![]() temos
temos
![\begin{displaymath}
\frac{2}{\left[N^d(\rho^2+\alpha_0)\right]^2}=\frac{\partial...
...yle \int [{\bf d} \varphi] e^{S[{\tilde{\varphi}}]} }
\right).
\end{displaymath}](img53.png)
Aqui devemos distinguir duas situações:
![]() e
e
![]() .
No primeiro caso efetuando as derivadas chegamos a
.
No primeiro caso efetuando as derivadas chegamos a
e no segundo caso
Generalizando para uma função de 2n pontos quaisquer temos, analogamente,
e
respectivamente para
![]() e
e
![]()
![]() . Esta propriedade nos leva a um
resultado físico interessante: como todos os observáveis da teoria
derivam das funções de n pontos e estas fatoram-se na função de dois
pontos, podemos concluir que neste modelo toda a física pode ser
abstraída desta função. Em outras palavras, a única física existente é
a propagação de ondas planas de massa física relacionada com o análogo
dimensional de
. Esta propriedade nos leva a um
resultado físico interessante: como todos os observáveis da teoria
derivam das funções de n pontos e estas fatoram-se na função de dois
pontos, podemos concluir que neste modelo toda a física pode ser
abstraída desta função. Em outras palavras, a única física existente é
a propagação de ondas planas de massa física relacionada com o análogo
dimensional de ![]() (pólo do propagador).
(pólo do propagador).