A Teoria Quântica de Campos na Rede Euclidiana

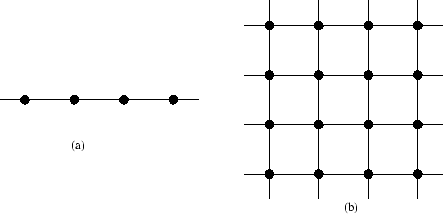
A rede Euclidiana em d dimensões e N vértices consiste de N pontos ou sítios ligados entre si por N conexões ou links em cada uma das d direções (fig. 3.1). Precisamos ainda distinguir entre links internos e links de borda, bem como escolher as condições de contorno para os links da borda. Um estudo detalhado destes objetos é apresentado na referência [9].

Neste projeto utilizamos condições periódicas de contorno.

Figure: Exemplos de rede Euclidiana com (a) dimensão d=1 e número de vértices N=4 e (b) dimensão d=2 e número de vértices N=4.

Os campos básicos são funções definidas em cada um dos sítios da rede, $\varphi(\vec{n})$. No caso do campo com uma única componente, por exemplo, o campo $\varphi$ atribui a cada sítio $\vec{n}$ da rede um valor que pode ser real, inteiro etc., dependendo do modelo estudado. Já os links estão associados com variações deste campo. Assim, por exemplo, temos a variável conhecida como diferença finita entre campos vizinhos

$$\Delta_{\mu} \varphi(\vec{n})\equiv \varphi(\vec{n} + \hat{n}_{\mu}) - \varphi(\vec{n}),$$

definida em cada link.

Para a construção da teoria nesta rede continuamos utilizando o formalismo de integração funcional. Assim definimos uma ``ação discretizada'' para o modelo

$$S=\sum_{sitios} {\cal L},$$ (3.1)

onde ${\cal{L}}$ e S são as suas densidade Lagrangiana e ação, respectivamente. Aplicamos aqui um único vínculo: que esta ação tenda à respectiva ação do modelo clássico correspondente no limite do contínuo. Desta maneira podemos definir os observáveis da teoria em uma rede com N^d sítios por

$$\left\langle {\cal O}\right\rangle_N \equiv \frac{\displayst... ...\varphi] e^{-S}}{\displaystyle \int [{\bf d} \varphi] e^{-S}}.$$ (3.2)

Para a função de dois pontos, por exemplo, a equação (3.2) torna-se

$$\left\langle \varphi(\vec{x}_1) \varphi(\vec{x}_2) \right\ra... ...ec{x}_2) e^{-S}}{\displaystyle \int [{\bf d} \varphi] e^{-S}}.$$

Ao tomarmos o limite do contínuo, retornando para o espaço de Minkowski, podemos identificar a expressão acima com a função de Green de dois pontos do modelo (2.4) desde que consideremos, em (2.2),

$$\rho\equiv \frac{\displaystyle 1}{\displaystyle \int [{\bf d} \varphi] e^{-S}}.$$