| E0 | = | 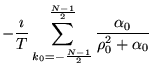 |
|
| = | 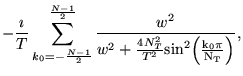 |
(4.15) |
Considerando o caso particular d=1 temos para a equação (4.12)
| E0 | = | 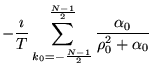 |
|
| = | 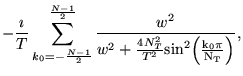 |
(4.15) |
onde
![]() e estamos
considerando uma rede ímpar.
e estamos
considerando uma rede ímpar.
Para analisar a expressão acima vamos inicialmente para o espaço de
Minkowski, através da rotação de Wick
![]() .
Neste
caso temos que
.
Neste
caso temos que
| E0 | = |  |
|
| = | 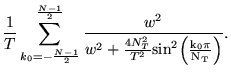 |
(4.16) |
Olhando para o comportamento da expressão acima no limite ![]() com N fixo, pode-se demonstrar que neste caso
com N fixo, pode-se demonstrar que neste caso ![]() .
.
Para w >> 1/T tomamos paralelamente o limite
![]() .
Neste caso
.
Neste caso ![]() .
Graficamente temos
a situação mostrada na figura (4.1).
.
Graficamente temos
a situação mostrada na figura (4.1).
Em analogia com a Mecânica Quântica, podemos mapear o resultado acima em um oscilador harmônico unidimensional de frequência w. Para baixas energias temos efeitos devidos ao tamanho finito da caixa, expressos pelo fator 1/T.
Para d>1 repetimos o análise acima, simplesmente substituindo w
por
![]() ,
chegando ao resultado para altos
valores de w e considerando o limite de tempo infinito,
,
chegando ao resultado para altos
valores de w e considerando o limite de tempo infinito,
onde
![]() ,
,
![]() e
e
![]() .
Esta
energia pode ser interpretada como sendo a soma de Nd-1
osciladores harmônicos unidimensionais, que no limite do contínuo é
divergente.
.
Esta
energia pode ser interpretada como sendo a soma de Nd-1
osciladores harmônicos unidimensionais, que no limite do contínuo é
divergente.