Limite do Contínuo

Agora estudaremos o limite do contínuo para a ação e o número de partículas. Antes de continuar porém precisamos avaliar no contexto deste trabalho o que significa este limite.

Temos a princípio três limites a considerar quando estamos trabalhando na rede: $N\rightarrow \infty$ , $\alpha_R \rightarrow 0$ e $\vec{k} \rightarrow$ modo on-shell. O primeiro deles é óbvio. O segundo está relacionado com a necessidade de se ir para a linha crítica no limite do contínuo, aonde $\alpha_R = 0$. O terceiro está diretamente relacionado com o projeto e condiz com a imposição da relação on-shell no limite do contínuo ou, em outras palavras, seleciona dentre todos os modos disponíveis aqueles que tem significado físico, com uma ``escada'' finita e positiva no limite do contínuo. A forma mais completa de ser pensar no limite do contínuo é a de se tomar estes três limites simultaneamente. Existem porém dificuldades numéricas ao se tentar fazer isso. Em primeiro lugar aumentar o tamanho da rede mantendo $\alpha_R \equiv \alpha_R(\alpha, \lambda, N)$ em valores especificados requer muito tempo computacional. Isso porque $\alpha_R$ é um observável a ser medido e não conhecemos a priori a relação exata entre ele e $\alpha$, $\lambda$ e N.

Além disso, com relação aos modos de Fourier, precisamos na análise daqueles que pelo menos tendam aos modos on-shell no limite do contínuo. Porém, a estrutura do código coleciona somente uma pequena parcela dos modos $\vec{k}$ existentes, sendo a maior parte sem este comportamento. Além disso, dentre os modos restantes, que tendem ao limite certo, a grande maioria é tipo space-like na rede finita. Isso não chega a ser um problema, mas certamente representa uma escolha específica de limites, ditada pelas atuais limitações numéricas e computacionais.

Paralelamente a esta discussão, para a análise do limite do contínuo precisamos também reduzir a qualidade da estatística por não termos recursos computacionais suficientes. Isso implica em um aumento no valor absoluto dos erros tanto na ação quanto na energia. Ainda assim para estes observáveis os erros são pequenos, da ordem de 2 por cento. Porém, estes erros aumentam consideravelmente para o operador ${\cal{N}}$ e para $\Delta E_n$, que são diferenças da ordem dos erros nos valores absolutos de S e E respectivamente. Esta parte do estudo, devido a esta restrição, será mais qualitativa que a anterior. Vale salientar que esta é uma dificuldade apenas prática, uma vez que como acabamos de observar em uma rede pequena, se tivermos possibilidade de aumentar a estatística, os resultados para a ``escada'' serão preservados.

Nesta fase foram executadas 100 submédias com 10000 iterações em cada uma delas. Analisamos redes de 4, 6, 8, e 10 vértices nos mesmos valores de parâmetros já estudados.

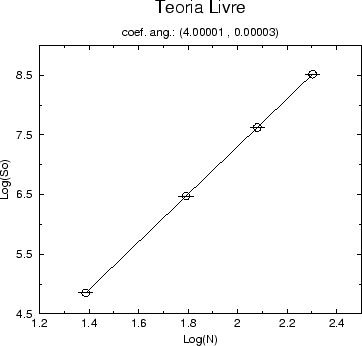
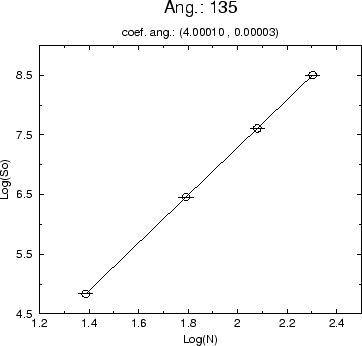
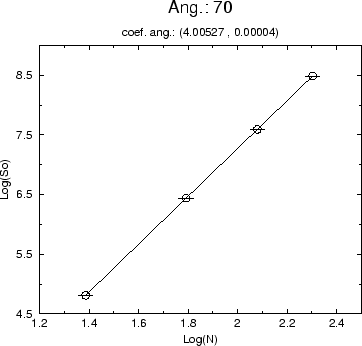
Para a ação, temos os gráficos (5.11) a (5.14) que expressam o seu comportamento no ensemble do vácuo para valores crescentes de N.

Figure: Gráfico do valor esperado da ação no vácuo como função do número de vértices N na teoria livre, em escala logarítmica. O coeficiente angular é o valor da dimensão espaço-temporal (eq. 4.8).

Figure: Gráfico do valor esperado da ação no vácuo como função do número de vértices N, em escala logarítmica, na teoria interagente com raio unitário e $\theta =135^0$. O coeficiente angular está relacionado com o valor da dimensão espaço-temporal.

Figure: Gráfico do valor esperado da ação no vácuo como função do número de vértices N, em escala logarítmica, na teoria interagente com raio unitário e $\theta =70^0$. O coeficiente angular está relacionado com o valor da dimensão espaço-temporal.

Figure: Gráfico do valor esperado da ação no vácuo como função do número de vértices N, em escala logarítmica, na teoria interagente com raio unitário e $\theta =35^0$. O coeficiente angular está relacionado com o valor da dimensão espaço-temporal.

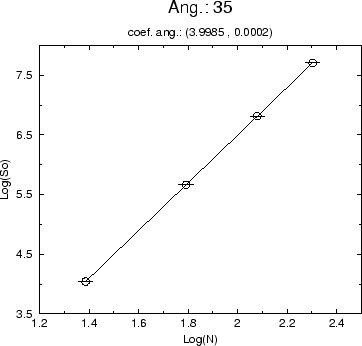Da expressão analítica para a ação no estado de vácuo (4.8) esperamos que o coeficiente angular de $\log(S_0)$ por $\log(N)$ seja 4, a dimensão espaço-temporal. O comportamento do valor absoluto do coeficiente linear não é relevante, uma vez que não está relacionado com a divergência.

O estudo do limite do contínuo para $\Delta {\cal N}$ não é factível com os dados e precisões disponíveis, pois requer uma análise do tipo

$$\theta_c(n)=\theta_c+\frac{\rm {const}}{N^p}$$

onde $\theta_c$, const e p estão por determinar. Mesmo assim o estudo qualitativo apresentado nas figuras (5.9) e (5.10) indica o comportamento correto.