



Next: Limite do Contínuo
Up: Cálculo do Número de
Previous: Cálculo do Número de
Contents
Para um estudo dos observáveis ação e número de partículas
foram executadas 1000 submédias e 100000 iterações em cada uma
delas. Nos gráficos
apresentados a seguir iremos trabalhar com as coordenadas polares r
e
Nos gráficos
apresentados a seguir iremos trabalhar com as coordenadas polares r
e 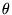 ao invés dos parâmetros
ao invés dos parâmetros 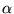 e
e 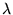 no espaço de
parâmetros do modelo. O ângulo
no espaço de
parâmetros do modelo. O ângulo 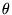 será definido de tal forma que
para
será definido de tal forma que
para 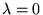 e
e 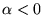 ,
,
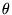 é nulo e para
é nulo e para 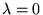 e
e
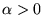 ,
,
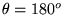 .
A direção adotada como temporal será a
última. Estaremos considerando na análise sempre o espaço-tempo
quadridimensional e o parâmetro raio (r) unitário.
.
A direção adotada como temporal será a
última. Estaremos considerando na análise sempre o espaço-tempo
quadridimensional e o parâmetro raio (r) unitário.
Inicialmente analisaremos a consistência do código através da teoria livre.
As figuras (5.1) e (5.2) apresentam os
resultados para a ação e para o
número de partículas calculados por simulação através das equações
(5.1), (5.2) e (5.3) neste caso.
Figure:
Gráfico do valor esperado da ação como função do número de
partículas na teoria livre calculados para o modo (0,0,0,1). Os
resultados foram obtidos por simulação estocástica em uma rede com 4
vértices no espaço-tempo quadridimensional.
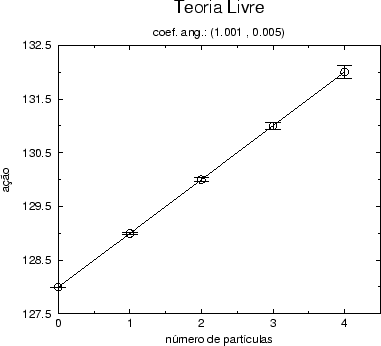 |
Figure:
Gráfico do número de partículas obtido por simulações
estocásticas como função do número de partículas analítico na teoria
livre, para o modo (0,0,0,1). Estamos considerando uma rede com 4
vértices no espaço-tempo quadridimensional.
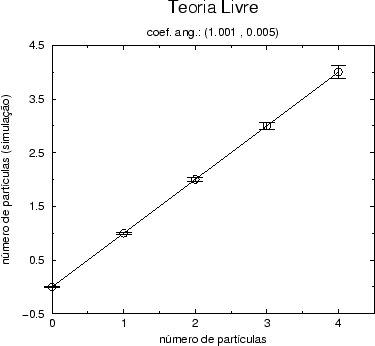 |
Para a teoria livre sabemos que a ação pode ser escrita analiticamente
como (4.9)
Assim, para d=4 e N=4 a ação calculada no vácuo é igual a 128, e o
valor da escada é unitário independentemente do modo, o que confere
com os dados apresentados.
Para a teoria interagente efetuamos rodadas em três posições
distintas: no meio da fase simétrica (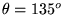 ), no meio da fase
quebrada (
), no meio da fase
quebrada (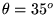 )
e nas proximidades da linha crítica pela fase
simétrica (
)
e nas proximidades da linha crítica pela fase
simétrica (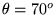 ). Os resultados obtidos para a ação e para o
número de partículas estão apresentados nos gráficos
(5.3) a (5.8).
). Os resultados obtidos para a ação e para o
número de partículas estão apresentados nos gráficos
(5.3) a (5.8).
Figure:
Gráfico do valor esperado da ação como função do número de
partículas na teoria interagente com 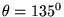 e r=1 calculados
para o modo (0,0,0,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1 calculados
para o modo (0,0,0,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
 |
Figure:
Gráfico do número de partículas obtido por simulações
estocásticas como função do número de partículas analítico na teoria
interagente com 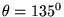 e r=1 para o modo (0,0,0,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1 para o modo (0,0,0,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
 |
Figure:
Gráfico do valor esperado da ação como função do número de
partículas na teoria interagente com 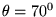 e r=1 calculados
para o modo (0,0,0,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1 calculados
para o modo (0,0,0,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
 |
Figure:
Gráfico do número de partículas obtido por simulações
estocásticas como função do número de partículas analítico na teoria
interagente com 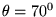 e r=1 para o modo (0,0,0,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1 para o modo (0,0,0,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
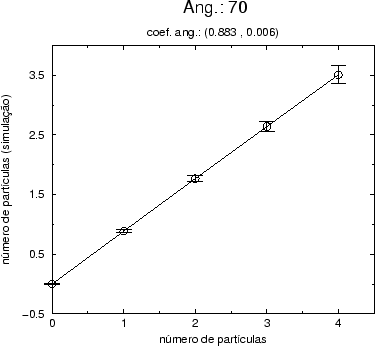 |
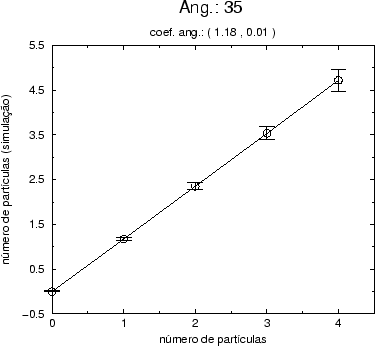
Figure:
Gráfico do valor esperado da ação como função do número de
partículas na teoria interagente com  e r=1 calculados
para o modo (0,0,0,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1 calculados
para o modo (0,0,0,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
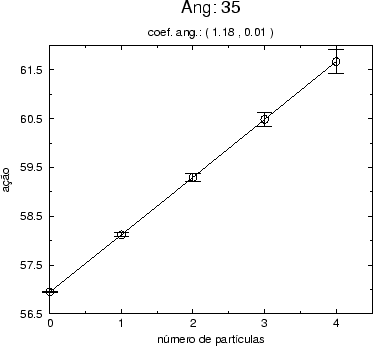 |
Figure:
Gráfico do número de partículas obtido por simulações
estocásticas como função do número de partículas analítico na teoria
interagente com  e r=1 para o modo (0,0,0,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1 para o modo (0,0,0,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
 |
Podemos perceber que os resultados da ação para o estado de vácuo na
teoria interagente não coincidem em valor absoluto com os
valores analíticos calculados na teoria livre,
NLd-1NT/2. Isso não é de todo inesperado,
porque agora estamos olhando para a teoria interagente. A nossa
expectativa é apenas que exista o mesmo comportamente divergente
no limite do contínuo. Esta análise será feita adiante.
Já para o observável número de partículas, em uma rede finita, assim
como para a ação, temos o comportamento qualitativo esperado, porém
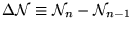 não é identicamente
unitário dentro da barra de erros. Podemos justificar este fato pela
necessidade de se olhar para o limite do contínuo. Entretanto, mesmo em
redes finitas e pequenas podemos estudar o comportamento de
não é identicamente
unitário dentro da barra de erros. Podemos justificar este fato pela
necessidade de se olhar para o limite do contínuo. Entretanto, mesmo em
redes finitas e pequenas podemos estudar o comportamento de
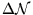 como função do ângulo
como função do ângulo 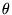 .
Os gráficos (5.9)
e (5.10) ilustram esta análise para N=4 e N=6
respectivamente. Note que em ambos os casos
.
Os gráficos (5.9)
e (5.10) ilustram esta análise para N=4 e N=6
respectivamente. Note que em ambos os casos
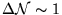 para
para
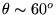 . Este resultado aponta em direção à linha
crítica do modelo para d=4, que corresponde a
. Este resultado aponta em direção à linha
crítica do modelo para d=4, que corresponde a
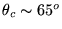 .
É de se esperar que no limite do contínuo,
.
É de se esperar que no limite do contínuo,
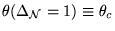 .
.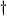 . Para uma
análise mais detalhada em redes finitas seria necessário um número
maior de pontos nos gráficos, o que não é fácil de se obter na
estatística que estamos analisando com os recursos computacionais
disponíveis.
. Para uma
análise mais detalhada em redes finitas seria necessário um número
maior de pontos nos gráficos, o que não é fácil de se obter na
estatística que estamos analisando com os recursos computacionais
disponíveis.
Figure:
Gráfico do coeficiente angular da escada do número de
partículas
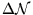 como função do ângulo
como função do ângulo
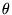 para o modo (0,0,0,1), com d=4 e N=4. Temos aqui um
indicativo de que o número de partículas torna-se inteiro (
para o modo (0,0,0,1), com d=4 e N=4. Temos aqui um
indicativo de que o número de partículas torna-se inteiro (
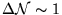 )
nas imediações da linha crítica do modelo
)
nas imediações da linha crítica do modelo
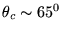 .
.
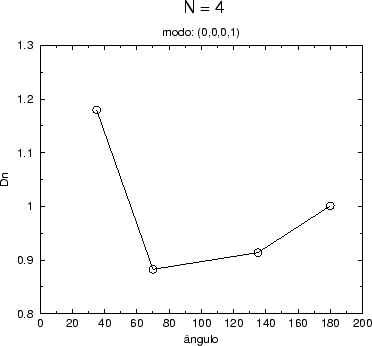 |
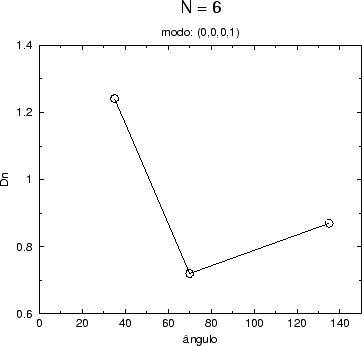
Figure:
Gráfico do coeficiente angular da escada do número de
partículas
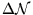 como função do ângulo
como função do ângulo
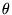 para o modo (0,0,0,1), com d=4 e N=6. Temos aqui um
indicativo de que o número de partículas torna-se inteiro (
para o modo (0,0,0,1), com d=4 e N=6. Temos aqui um
indicativo de que o número de partículas torna-se inteiro (
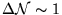 )
nas imediações da linha crítica do modelo
)
nas imediações da linha crítica do modelo
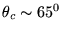 .
.
 |




Next: Limite do Contínuo
Up: Cálculo do Número de
Previous: Cálculo do Número de
Contents
![]() Nos gráficos
apresentados a seguir iremos trabalhar com as coordenadas polares r
e
Nos gráficos
apresentados a seguir iremos trabalhar com as coordenadas polares r
e ![]() ao invés dos parâmetros
ao invés dos parâmetros ![]() e
e ![]() no espaço de
parâmetros do modelo. O ângulo
no espaço de
parâmetros do modelo. O ângulo ![]() será definido de tal forma que
para
será definido de tal forma que
para ![]() e
e ![]() ,
,
![]() é nulo e para
é nulo e para ![]() e
e
![]() ,
,
![]() .
A direção adotada como temporal será a
última. Estaremos considerando na análise sempre o espaço-tempo
quadridimensional e o parâmetro raio (r) unitário.
.
A direção adotada como temporal será a
última. Estaremos considerando na análise sempre o espaço-tempo
quadridimensional e o parâmetro raio (r) unitário.


![]() ), no meio da fase
quebrada (
), no meio da fase
quebrada (![]() )
e nas proximidades da linha crítica pela fase
simétrica (
)
e nas proximidades da linha crítica pela fase
simétrica (![]() ). Os resultados obtidos para a ação e para o
número de partículas estão apresentados nos gráficos
(5.3) a (5.8).
). Os resultados obtidos para a ação e para o
número de partículas estão apresentados nos gráficos
(5.3) a (5.8).






![]() não é identicamente
unitário dentro da barra de erros. Podemos justificar este fato pela
necessidade de se olhar para o limite do contínuo. Entretanto, mesmo em
redes finitas e pequenas podemos estudar o comportamento de
não é identicamente
unitário dentro da barra de erros. Podemos justificar este fato pela
necessidade de se olhar para o limite do contínuo. Entretanto, mesmo em
redes finitas e pequenas podemos estudar o comportamento de
![]() como função do ângulo
como função do ângulo ![]() .
Os gráficos (5.9)
e (5.10) ilustram esta análise para N=4 e N=6
respectivamente. Note que em ambos os casos
.
Os gráficos (5.9)
e (5.10) ilustram esta análise para N=4 e N=6
respectivamente. Note que em ambos os casos
![]() para
para
![]() . Este resultado aponta em direção à linha
crítica do modelo para d=4, que corresponde a
. Este resultado aponta em direção à linha
crítica do modelo para d=4, que corresponde a
![]() .
É de se esperar que no limite do contínuo,
.
É de se esperar que no limite do contínuo,
![]() .
.![]() . Para uma
análise mais detalhada em redes finitas seria necessário um número
maior de pontos nos gráficos, o que não é fácil de se obter na
estatística que estamos analisando com os recursos computacionais
disponíveis.
. Para uma
análise mais detalhada em redes finitas seria necessário um número
maior de pontos nos gráficos, o que não é fácil de se obter na
estatística que estamos analisando com os recursos computacionais
disponíveis.

