Limite do Contínuo

Como já foi dito antes, o limite do contínuo não pode ser avaliado com grande precisão com os recursos disponíveis. Faremos portanto o seguinte: mantendo $\alpha$ e $\lambda$ constantes aumentamos o tamanho da rede e estudamos o comportamento de $\Delta E_{\vec{k}}$ nesta situação para os modos que tendam ao limite on-shell no contínuo. Um modo disponível computacionalmente e que tem estas propriedades é o (0,0,1,1). Nele portanto baseamos nossa análise.

Iniciemos o estudo com a teoria livre. Neste caso temos dois conjuntos de dados. Um com os valores obtidos via simulação para $\Delta E_{\vec{k}}$ por N, que denotamos $\Delta E_{\vec{k}}^{\rm {sim}}$, e outro, calculado a partir da equação (4.14). Para comparar estes dois conjuntos de dados vamos aproximar $\Delta E_{\vec{k}}^{\rm {sim}}$ pela expressão

$$f_N\equiv A + B X$$ (5.4)

onde

$$X\equiv \left( \frac{-\rho^2_0 +{\mbox{\boldmath$\mathfrak{\rho}$}}^2 + \alpha_R}{\rho^2 + \alpha_R} \right)_{\vec{k}}.$$

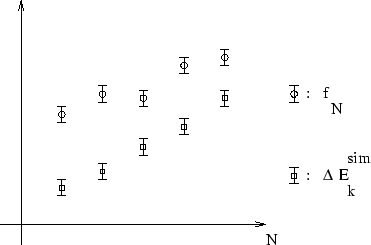
Agora considerando que $f_N \equiv f_N \pm \sigma_{f_N}$, por propagação de erros em $\alpha_R$ queremos encontrar os valores de A e B que mais aproximam $\Delta E_{\vec{k}}^{\rm {sim}}$ de f ponderando os respectivos erros. A figura (5.19) expressa estas idéias.

Figure: Ajuste dos valores medidos do coeficiente angular da escada de energia $\Delta E_{\vec{k}}^{\rm {sim}}$ em comparação com f_N expresso por (5.4). Devemos encontrar o valor de B que mais aproxime as duas coleções de dados como função de N.

Efetuando esta ``propagação de erros'' encontramos, no caso da teoria livre, $B=(1.0 \pm 0.4)$.

Para a teoria interagente, considerando $\alpha_0\equiv\alpha_R$ encontramos, para $\theta =135^0$, $B=(1.0\pm0.3)$; para $\theta =70^0$, $B=(-3 \pm 6)$; para $\theta =35^0$, $B=(1.1\pm1.6)$. Apesar dos erros serem grandes, os valores obtidos estão conforme esperado: para B=1 os valores medidos concordariam perfeitamente com os valores analíticos.