Os Erros

Um fato interessante a ser observado é a diferença entre os valores dos erros entre o ensemble do vácuo e os ensembles de n partículas. Como exemplo considere o gráfico (5.1) da ação na teoria livre para o modo (0,0,0,1) em N=4. Neste caso $S_0=(127.998 \pm 0.001)$ e $S_1=(129.00 \pm 0.02)$. O aumento relativo dos erros entre S₁ e S₂, S₂ e S₃ etc, é facilmente justificado considerando que é mais fácil medir funções de dois pontos do que de quatro, seis e oito pontos, pois estas são características progressivamente mais delicadas e sutis da distribuição. Mas porque não temos o mesmo aumento dos erros entre os observáveis no vácuo e no estado de uma partícula? Isso acontece devido à forma com que estamos medindo os observáveis em cada caso. Para o cálculo de E₀, os observáveis medidos são

$$\left\langle \sum_s \left( \Delta_{\mu} \varphi \right)^2 \right\rangle,$$

$$\left\langle \sum_s \varphi^2 \right\rangle$$

e

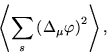
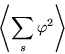
$$\left\langle \sum_s \varphi^4 \right\rangle.$$

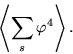
Considerando o segundo deles, por exemplo, temos que

$$\left\langle \sum_s \varphi^2 \right\rangle=\sum_s \left\lan... ...right\rangle=N_L^{d-1}N_T \left\langle \varphi^2 \right\rangle$$

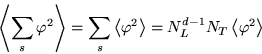
por invariança translacional, portanto

$$\delta \left\langle \sum_s \varphi^2 \right\rangle \propto \... ...{N^{\frac{d}{2}}} \delta \left\langle \varphi^2 \right\rangle.$$ (5.5)

Já no cálculo de E_n os observáveis utilizados são

$$\left\langle {\vert \tilde{\varphi}_k \vert}^{2n} \right\rangle,$$

$$\left\langle \sum_s \left( \Delta_{\mu} \varphi \right)^2 {\vert \tilde{\varphi}_k \vert}^{2n} \right\rangle,$$

$$\left\langle \sum_s \varphi^2 {\vert \tilde{\varphi}_k \vert}^{2n}\right\rangle$$

e

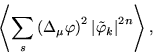
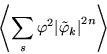
$$\left\langle \sum_s \varphi^4 {\vert \tilde{\varphi}_k \vert}^{2n}\right\rangle.$$

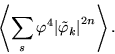
Considerando a função de 2 pontos como exemplo temos que

$$\left\langle {\vert \tilde{\varphi}_k \vert}^{2}\right\rangl... ...} \left\langle \varphi(\vec{x}) \varphi(\vec{y})\right\rangle,$$

que não pode ser fatorada em uma média de $\left\langle\varphi(\vec{x})\right\rangle^2$. Assim E₀ e E₁ devem ter erros relativos que, conforme (5.5), diferem por um fator de escala da ordem de $N^{\frac{d}{2}}$, ou seja,

$$\frac{\sigma_{S_0} S_1} {\sigma_{S_1} S_0} \propto \frac{1}{N^{\frac{d}{2}}}.$$ (5.6)

Para observar este comportamento vamos olhar os valores dos erros relativos em tamanhos crescentes de rede. A figura (5.20) apresenta os resultados.

Figure: Gráfico em escala logarítmica da razão dos erros relativos entre a ação no vácuo e no estado de uma partícula, como função de N (eq. 5.6), para o modo (1,0,0,0). O coeficiente angular esperado é $-d/2 \equiv -2$.

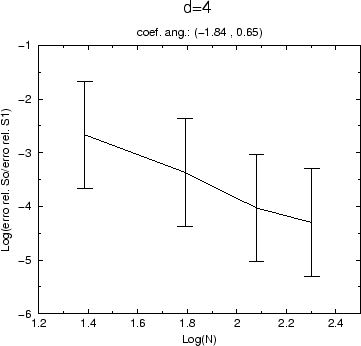O valor medido para o coeficiente angular $(-1.84 \pm 0.65)$ confere com o esperado, já que na escala logarítmica o valor do coeficiente angular deve ser, por (5.6), igual a -2.