Resultados

Novamente calculamos 1000 submédias com 100000 iterações cada uma delas em uma rede pequena (N=4 e r=1). Nos gráficos apresentados estaremos considerando, por simplicidade, $T \equiv 1$ .

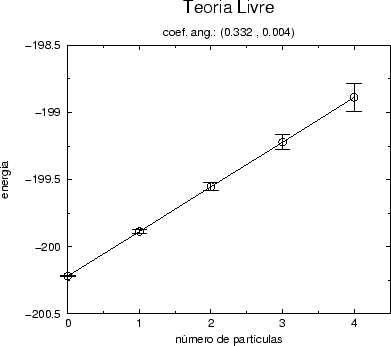
No caso da teoria livre temos inicialmente o gráfico (5.15) para a energia $E_{\vec{k},n}$ pelo número de partículas.

**Figure:** Gráfico da energia como função do número de partículas na teoria livre, calculados para o modo (0,0,0,1). Os resultados foram obtidos por simulação estocástica em uma rede com 4 vértices no espaço-tempo quadridimensional.
$\begin{figure}\centering\epsfig{file=ps/esc_en_t180_m0001.epsf,scale=0.5,angle=0} \end{figure}$

Os valores analíticos exatos para a teoria livre para os observáveis E₀ e $\Delta E_{\vec{k}}$ foram calculados a partir das equações (4.12) e (4.14) sendo para o modo (0,0,0,1) iguais a $-\imath E_0=-200.22$ e $-\imath \Delta E_{\vec{k}}=0.33$ , ou seja, concordam com o obtido por simulação.

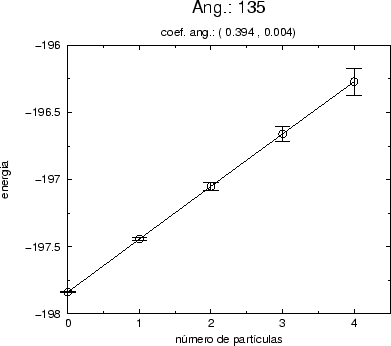
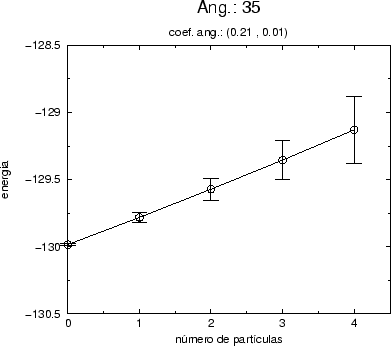
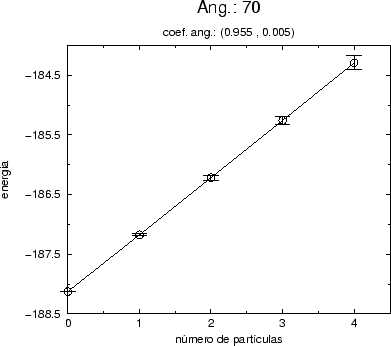
Para a fase simétrica temos o gráfico (5.16), para a fase quebrada o gráfico (5.17) e para as proximidades da linha crítica o gráfico (5.18).

**Figure:** Gráfico da energia como função do número de partículas na teoria interagente com $\theta =135^0$ e r=1, calculados para o modo (0,0,0,1). Os resultados foram obtidos por simulação estocástica em uma rede com 4 vértices no espaço-tempo quadridimensional.
$\begin{figure}\centering\epsfig{file=ps/esc_en_t135_m0001.epsf,scale=0.5,angle=0} \end{figure}$

**Figure:** Gráfico da energia como função do número de partículas na teoria interagente com $\theta =35^0$ e r=1, calculados para o modo (0,0,0,1). Os resultados foram obtidos por simulação estocástica em uma rede com 4 vértices no espaço-tempo quadridimensional.
$\begin{figure}\centering\epsfig{file=ps/esc_en_t035_m0001.epsf,scale=0.5,angle=0} \end{figure}$

**Figure:** Gráfico da energia como função do número de partículas na teoria interagente com $\theta =70^0$ e r=1, calculados para o modo (0,0,0,1). Os resultados foram obtidos por simulação estocástica em uma rede com 4 vértices no espaço-tempo quadridimensional.
$\begin{figure}\centering\epsfig{file=ps/esc_en_t070_m0001.epsf,scale=0.5,angle=0} \end{figure}$

Para interpretar os valores na teoria interagente podemos compará-los com os respectivos valores analíticos para a teoria livre simplesmente substituindo $\alpha$ pelo valor de $\alpha_R$ calculado via simulação. Faremos uma análise detalhada mais adiante, quando tomarmos o limite do contínuo. Por enquanto vamos apenas explorar os dois resultados. Para a fase simétrica, por exemplo, os valores ``analíticos'' obtidos são para o modo (0,0,0,1) $-\imath E_0=-200.05$ e $\imath \Delta E_{\vec{k}}=0.35$ . Estes resultados não concordam com os obtidos via simulação dentro da barra de erros (diferem da ordem de dois por cento). A princípio espera-se que $\alpha_R$ assuma o papel de $\alpha_0$ somente em primeira aproximação para redes finitas pois este comportamento é esperado apenas no limite do contínuo. Portanto o fato dos valores não estarem concordando perfeitamente em N=4 indica apenas o próximo passo a ser tomado na análise dos dados, o de ir em direção ao limite do contínuo, fato já detectado nos observáveis anteriores.