On the Sums of Inverse Even Powers of
Zeros of Regular Bessel Functions

Jorge L. deLyra

Department of Mathematical Physics, Physics Institute, University of São Paulo

February 18, 2013

Abstract:

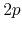
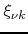
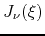
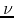
We provide a new, simple general proof of the formulas giving the infinite sums $\sigma(p,\nu)$ of the inverse even powers $2p$ of the zeros $\xi_{\nu k}$ of the regular Bessel functions $J_{\nu}(\xi)$, as functions of $\nu$. We also give and prove a general formula for certain linear combinations of these sums, which can be used to derive the formulas for $\sigma(p,\nu)$ by purely linear-algebraic means, in principle for arbitrarily large powers. 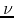We prove that these sums are always given by a ratio of two polynomials on $\nu$, with integer coefficients. 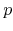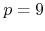We complete the set of known formulas for the smaller values of $p$, extend it to $p=9$, and point out a connection with the Riemann zeta function, which allows us to calculate some of its values.