Next: Using the Residue Theorem Up: On the Sums of Previous: Properties of
Let us consider now the proof that the integral is zero. In order to do
this we will separate the circuit in sections and prove the result for
each section. The complete circuit ![]() consists of two straight sections
consists of two straight sections
![]() e
e ![]() , of the great semicircle
, of the great semicircle ![]() and of two small
semicircles
and of two small
semicircles ![]() e
e ![]() of radius
of radius ![]() around the point
around the point
![]() .
.
For the pair of straight lines ![]() e
e ![]() , where we have
, where we have
![]() with
with
![]() , taking into account the orientation, we may write
, taking into account the orientation, we may write
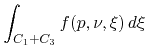 |
|||
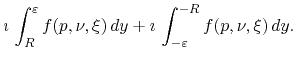 |
(23) |
Making in the second integral the transformation of variables
![]() , which implies
, which implies ![]() e
e ![]() , and since
, and since ![]() is odd, we have
is odd, we have
| (24) |
We see therefore that this part of the integral vanishes exactly,
independently of the values of ![]() and
and ![]() . We are therefore
free to take limits involving
. We are therefore
free to take limits involving ![]() or
or ![]() during the calculation
of the other sections of the integral, without affecting this result.
during the calculation
of the other sections of the integral, without affecting this result.
Next we consider the two semicircles of radius ![]() . We will
denote this part of the integral, to be calculated according to the
criterion of the principal value of Cauchy, as
. We will
denote this part of the integral, to be calculated according to the
criterion of the principal value of Cauchy, as
| (25) |
Since the function ![]() has a simple pole at
has a simple pole at ![]() , and is
also odd, it can be expressed as a Laurent series around this point, with
the form
, and is
also odd, it can be expressed as a Laurent series around this point, with
the form
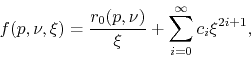 |
(26) |
where ![]() is the residue of the function at this point, and
is the residue of the function at this point, and
![]() are certain finite coefficients. The series is convergent so long
as
are certain finite coefficients. The series is convergent so long
as ![]() is smaller than the first zero
is smaller than the first zero ![]() . The sum of
positive powers represents an analytical function around
. The sum of
positive powers represents an analytical function around ![]() , and is
therefore regular within the circle of radius
, and is
therefore regular within the circle of radius ![]() . It follows
that the integral of this regular part goes to zero in the limit
. It follows
that the integral of this regular part goes to zero in the limit
![]() , since in this limit both each individual term of the
sum and the measure of the domain of integration vanish.
, since in this limit both each individual term of the
sum and the measure of the domain of integration vanish.
It follows that only the integral of the term containing the pole can
remain different from zero in the
![]() limit. We will
therefore calculate this integral in polar coordinates, with
limit. We will
therefore calculate this integral in polar coordinates, with
![]() and
and
![]() . Since we must use here the
Cauchy principal value we have for this part
. Since we must use here the
Cauchy principal value we have for this part
![]() of
the integral
of
the integral
![]() ,
,
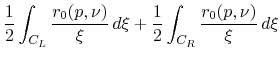 |
|||
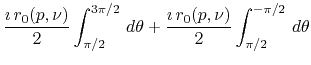 |
|||
| (27) |
Therefore, this part of the integral
![]() also vanishes, and
hence the integral
also vanishes, and
hence the integral
![]() vanishes in the limit
vanishes in the limit
![]() . Since during this deformation of the circuit no singularities of the
function are crossed, and hence the integral does not change, if follows
that the integral is zero for all values of
. Since during this deformation of the circuit no singularities of the
function are crossed, and hence the integral does not change, if follows
that the integral is zero for all values of ![]() smaller than
smaller than
![]() .
.
The last section of the circuit we must consider is ![]() . In this case
the integral is not zero for finite values of
. In this case
the integral is not zero for finite values of ![]() , but we may show that it
goes to zero in the limit
, but we may show that it
goes to zero in the limit ![]() , subject to the condition that for
large values of
, subject to the condition that for
large values of ![]() we have that Eq. (4) holds, so that the
circuit does not go over any of the singularities at the points
we have that Eq. (4) holds, so that the
circuit does not go over any of the singularities at the points ![]() . Using once more polar coordinates, in this section of the circuit
we have
. Using once more polar coordinates, in this section of the circuit
we have
![]() , where
, where
![]() ,
so that the integral is given by
,
so that the integral is given by
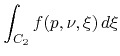 |
|||
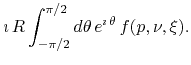 |
(28) |
Taking the absolute value of the integral and using the triangle inequalities we have
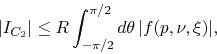 |
(29) |
for any value of ![]() , and hence also in the
, and hence also in the ![]() limit. We must
now consider the behavior of the absolute value of
limit. We must
now consider the behavior of the absolute value of ![]() for
large values of
for
large values of ![]() . In order to do this we calculate the limit
. In order to do this we calculate the limit
![$\displaystyle \lim_{R\to\infty}
\left[
R\int_{-\pi/2}^{\pi/2}d\theta\,
\vert f(p,\nu,\xi)\vert
\right]$](img124.png) |
|||
![$\displaystyle \lim_{R\to\infty}
\left[
R\int_{-\pi/2}^{\pi/2}d\theta\,
\frac{1}{R^{p+1}}\,
\left\vert\frac{J_{\nu+p}(\xi)}{J_{\nu}(\xi)}\right\vert
\right].$](img125.png) |
(30) |
As we established before, the limit of the absolute value of the ratio of
the two Bessel functions is ![]() . As a consequence of this, we have for the
integral over the section
. As a consequence of this, we have for the
integral over the section ![]() of the circuit, in the
of the circuit, in the ![]() limit,
limit,
![$\displaystyle \lim_{R\to\infty}
\left[
\int_{-\pi/2}^{\pi/2}d\theta\,
\frac{1}{R^{p}}
\right]$](img126.png) |
|||
| (31) |
since we have ![]() . This implies, of course, that
. This implies, of course, that ![]() in the
in the
![]() limit. We see therefore that the integral of
limit. We see therefore that the integral of ![]() over the circuit
over the circuit ![]() , in the
, in the ![]() limit, vanishes in all sections
of the circuit, and hence that the integral is zero in the
limit, vanishes in all sections
of the circuit, and hence that the integral is zero in the ![]() limit,
limit,
| (32) |