Next: Evaluation of the Integral Up: On the Sums of Previous: Definition of the Elements
Let us establish a few important properties of ![]() , starting by
its behavior under the inversion of the sign of
, starting by
its behavior under the inversion of the sign of ![]() . We start with the
analogous property of
. We start with the
analogous property of ![]() , for which we have, using the
Maclaurin series for these functions [3], which converges over
the whole complex plane,
, for which we have, using the
Maclaurin series for these functions [3], which converges over
the whole complex plane,
| (5) |
Using this in the expression for ![]() we get
we get
| (6) |
that is, ![]() is an odd function of
is an odd function of ![]() , for all
, for all ![]() and all
and all
![]() .
.
Next we show that ![]() has a simple pole at
has a simple pole at ![]() . Since
. Since
![]() ,
, ![]() and
and ![]() are analytical functions
over the whole complex-
are analytical functions
over the whole complex-![]() plane, it follows that
plane, it follows that ![]() is
analytical over the whole plane except for those points where the
denominator vanishes, where it has poles. These are the origin
is
analytical over the whole plane except for those points where the
denominator vanishes, where it has poles. These are the origin ![]() and
the zeros
and
the zeros ![]() of the Bessel function in the denominator. Note
that while for non-integer
of the Bessel function in the denominator. Note
that while for non-integer ![]() and
and ![]() the functions involved have
branching points at
the functions involved have
branching points at ![]() , the function
, the function ![]() never does. In
order to determine the residue of
never does. In
order to determine the residue of ![]() at
at ![]() we consider
the limit
we consider
the limit
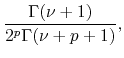 |
(7) |
where ![]() is the gamma function and we used once more the
Maclaurin series for
is the gamma function and we used once more the
Maclaurin series for ![]() . Since the limit is finite and
non-zero, it follows that
. Since the limit is finite and
non-zero, it follows that ![]() has a simple pole at
has a simple pole at ![]() , and
that
, and
that ![]() is the corresponding residue. Turning to the poles at
is the corresponding residue. Turning to the poles at
![]() , since
, since ![]() is a simple zero of
is a simple zero of ![]() , at
which its derivative
, at
which its derivative ![]() is different from zero, it follows
that
is different from zero, it follows
that ![]() has a Taylor expansion around this point, with the
form
has a Taylor expansion around this point, with the
form
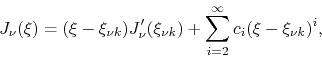 |
(8) |
for certain finite coefficients ![]() . In order to determine the residue
of
. In order to determine the residue
of ![]() at
at ![]() we consider then the limit
we consider then the limit
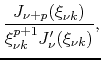 |
(9) |
where we used this Taylor expansion. Since the derivative is finite and
non-zero at ![]() , this limit also is finite and non-zero, and
hence it follows that
, this limit also is finite and non-zero, and
hence it follows that ![]() has a simple pole at
has a simple pole at ![]() ,
and that
,
and that ![]() is the corresponding residue. We can simplify this
expression using the well-known identity [4]
is the corresponding residue. We can simplify this
expression using the well-known identity [4]
| (10) |
which applied at
![]() , since
, since
![]() ,
results in
,
results in
| (11) |
It follows therefore that we have for the residues of the poles at
![]() ,
,
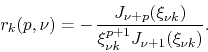 |
(12) |
We will now establish the behavior of the absolute value of the ratio of
Bessel functions which is contained in the expression of ![]() in
Eq. (3), for large values of
in
Eq. (3), for large values of ![]() . In order to do this we use
the asymptotic expansion of the Bessel functions [5], valid in
the whole complex plane so long as
. In order to do this we use
the asymptotic expansion of the Bessel functions [5], valid in
the whole complex plane so long as
![]() , written in terms
of
, written in terms
of ![]() and
and
![]() , to the lowest orders, and with the
trigonometric functions expressed as complex exponentials,
, to the lowest orders, and with the
trigonometric functions expressed as complex exponentials,
where
![]() and
and
![]() are certain limited
functions of
are certain limited
functions of ![]() and
and
![]() is a certain real number,
given by
is a certain real number,
given by
| (14) |
The behavior of the expression in Eq. (13) for large values of
![]() depends on the sign of
depends on the sign of ![]() , and the particular case
, and the particular case ![]() has to be examined separately. In this particular case we have
has to be examined separately. In this particular case we have
![$\displaystyle \sqrt{\frac{2}{\pi R}}
\left\{
\left[
1
+
\frac{{\cal R}_{c}(\nu,\xi)}{R^{2}}
\right]
\cos[\alpha(R,0,\nu)]
\right.
+$](img66.png) |
|||
![$\displaystyle \hspace{3.95em}
-
\left.
\left[
\frac{4\nu^{2}-1}{8R}
+
\frac{{\cal R}_{s}(\nu,\xi)}{R^{3}}
\right]
\sin[\alpha(R,0,\nu)]
\right\},$](img67.png) |
(15) |
where all the functions involved are now limited, so that for large values
of ![]() we have for the dominant part of
we have for the dominant part of ![]() ,
,
| (16) |
Note now that the points where
![]() are the zeros of
are the zeros of
![]() , expressed in the asymptotic limit. We will now choose a
way to take the
, expressed in the asymptotic limit. We will now choose a
way to take the ![]() limit such that these zeros are avoided. We
may simply chose for the passage of the circuit across the real axis that
point between two zeros where
limit such that these zeros are avoided. We
may simply chose for the passage of the circuit across the real axis that
point between two zeros where
![]() and
and
![]() . Since for
. Since for ![]() we have
we have
| (17) |
and we must have
![]() for some integer
for some integer ![]() , we conclude
that Eq. (4) holds, which will cause the crossing of the
circuit and the real axis to avoid the zeros. This defines the
, we conclude
that Eq. (4) holds, which will cause the crossing of the
circuit and the real axis to avoid the zeros. This defines the
![]() limit in full detail. It follows that for our purposes here
we may write the asymptotic expansion in the case
limit in full detail. It follows that for our purposes here
we may write the asymptotic expansion in the case ![]() as
as
![\begin{displaymath}
J_{\nu}(\xi)
=
\pm
\sqrt{\frac{2}{\pi R}}
\left[
1
+
\frac{{\cal R}_{c}(\nu,\xi)}{R^{2}}
\right].
\end{displaymath}](img74.png) |
(18) |
In the case ![]() we put the dominant real exponential in evidence
and obtain
we put the dominant real exponential in evidence
and obtain
![$\displaystyle \sqrt{\frac{\,e^{-\imath\,\theta}}{2\pi R}}\,e^{R\sin(\theta)}
\l...
...\frac{{\cal R}_{c}(\nu,\xi)}{R^{2}\,e^{\imath\,2\theta}}
\right]
\right.
\times$](img76.png) |
|||
![$\displaystyle \hspace{8em}
\times
\left.
\left[
e^{-2R\sin(\theta)}\,e^{\imath\,\alpha(R,\theta,\nu)}
+
e^{-\imath\,\alpha(R,\theta,\nu)}
\right]
\right.
+$](img77.png) |
|||
![$\displaystyle \hspace{6.05em}
+
\imath\,
\left.
\left[
\frac{4\nu^{2}-1}{8R\,e^...
...\frac{{\cal R}_{s}(\nu,\xi)}{R^{3}\,e^{\imath\,3\theta}}
\right]
\right.
\times$](img78.png) |
|||
![$\displaystyle \hspace{8em}
\times
\left.
\left[
e^{-2R\sin(\theta)}\,e^{\imath\...
...eta,\nu)}
-
e^{-\imath\,\alpha(R,\theta,\nu)}
\right]
\rule{0em}{4ex}
\right\},$](img79.png) |
(19) |
where all the functions within the brackets are now limited or go to zero
in the ![]() limit. Finally, we do the same thing for the case
limit. Finally, we do the same thing for the case
![]() , obtaining
, obtaining
![$\displaystyle \sqrt{\frac{\,e^{-\imath\,\theta}}{2\pi R}}\,e^{-R\sin(\theta)}
\...
...\frac{{\cal R}_{c}(\nu,\xi)}{R^{2}\,e^{\imath\,2\theta}}
\right]
\right.
\times$](img81.png) |
|||
![$\displaystyle \hspace{8.5em}
\times
\left.
\left[
e^{\imath\,\alpha(R,\theta,\nu)}
+
e^{2R\sin(\theta)}\,e^{-\imath\,\alpha(R,\theta,\nu)}
\right]
\right.
+$](img82.png) |
|||
![$\displaystyle \hspace{6.6em}
+
\imath\,
\left.
\left[
\frac{4\nu^{2}-1}{8R\,e^{...
...\frac{{\cal R}_{s}(\nu,\xi)}{R^{3}\,e^{\imath\,3\theta}}
\right]
\right.
\times$](img83.png) |
|||
![$\displaystyle \hspace{8.5em}
\times
\left.
\left[
e^{\imath\,\alpha(R,\theta,\n...
...n(\theta)}\,e^{-\imath\,\alpha(R,\theta,\nu)}
\right]
\rule{0em}{4ex}
\right\},$](img84.png) |
(20) |
where once more all the functions within the brackets are now limited or
go to zero in the ![]() limit. We are now in a position to analyze
the behavior of the absolute value of the ratio of two Bessel functions
which appears in the definition of
limit. We are now in a position to analyze
the behavior of the absolute value of the ratio of two Bessel functions
which appears in the definition of ![]() . The factors which do
not depend on
. The factors which do
not depend on ![]() are common to the numerator and denominator, and
cancel out. In the case
are common to the numerator and denominator, and
cancel out. In the case ![]() we get
we get
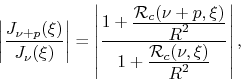 |
(21) |
so that in the ![]() limit we get
limit we get
| (22) |
It is not difficult to verify that for both the case ![]() and the
case
and the
case ![]() we get this same value for this limit. We see therefore
that the
we get this same value for this limit. We see therefore
that the ![]() limit of the absolute value of this ratio is simply
limit of the absolute value of this ratio is simply
![]() , for all values of
, for all values of ![]() in
in ![]() .
.