Definition of the Elements Involved

The proof will be based on the singularity structure of the following analytical function in the complex-$\xi$ plane,

$$f(p,\nu,\xi) = \frac{J_{\nu+p}(\xi)}{\xi^{p+1}J_{\nu}(\xi)},$$ (3)

where for the time being we may consider that $\nu\geq 0$ and $p>0$ are real numbers. In case any of the functions involved have branching points at $\xi=0$, we consider the cuts to be over the negative real semi-axis. Preliminary to the proof, it will be necessary to establish a few properties of this function.

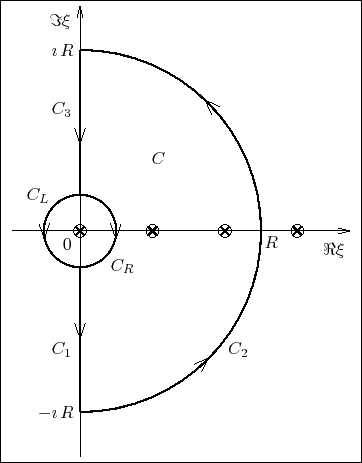
We will consider the contour integral of this function over the circuit on the complex-$\xi$ plane shown in Fig. 1, in the $R\to\infty$ limit. Since this circuit goes through the origin $\xi=0$, where the function will be seen to have a simple pole, we will adopt for the integral the principal value of Cauchy. The limit $R\to\infty$ will be taken in a discrete way, in order to avoid going through the other singularities of the function, which are located at $\xi=\xi_{\nu k}$. We will see that, for large values of $R$ and $j$, it is possible to adopt for $R$ the values given by

$$R = \pi\,\frac{2\nu+1}{4} + j\pi,$$ (4)

where for each $k$ there is a value of the integer $j$ such that $R$ is strictly within the interval $(\xi_{\nu k},\xi_{\nu (k+1)})$. In this way each step in the discrete $R\to\infty$ limit will correspond to a partial sum of the infinite sums involved.

Figure 1: The integration contour in the complex-$\xi$ plane, showing the various parts of the circuit $C$ and some of the singularities of $f(p,\nu ,\xi )$.

The proof of the expressions for $\sigma(p,\nu)$ consists of two parts: first, the proof that the integral of $f(p,\nu ,\xi )$ over the circuit is zero in the $R\to\infty$ limit, for all $p>0$ and all $\nu\geq 0$; second, the use of the residue theorem. This will result in a general formula from which the expressions for the sums $\sigma(p,\nu)$ can be derived. We will also present a partial solution of the problem of deriving the formulas for $\sigma(p,\nu)$, which will take the form of another general formula from which these expressions can be derived algebraically.