Introduction

In boundary value problems involving the diffusion equation the following infinite sums sometimes appear,

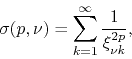$$\sigma(p,\nu) = \sum_{k=1}^{\infty} \frac{1}{\xi_{\nu k}^{2p}},$$ (1)

most often for $p=1$, where $\xi_{\nu k}$ are the positions of the zeros located away from the origin of the regular cylindrical Bessel function $J_{\nu}(\xi)$, with real $\nu\geq 0$ and integer $p>0$. The sums are convergent for $p\geq 1$. As we will show in what follows, all these sums have the property that they are given by the ratio of two polynomials on $\nu$ with integer coefficients. The simplest and most common example is

$$\sigma(1,\nu) = \frac{1}{4(\nu+1)}.$$ (2)

In a few cases the exact expression of these polynomials are available in the literature [1]. The known cases are those obtained by Rayleigh, extending investigations by Euler, for $p=1$ through $p=5$, and one discovered by Cayley, for $p=8$. The cases $p=6$ and $p=7$ seem not to be generally known, and will be given explicitly further on. The known cases were obtained in a case-by-case fashion, using the expression of the Bessel functions as infinite products involving its zeros.

In this paper we will provide a simple, independent proof of all the known formulas, and will present a general formula from which the specific formulas can be derived, for any given strictly positive integer value of $p$, by purely algebraic means. The proof will rely entirely on the general properties of analytical functions and on the well-known properties of the functions $J_{\nu}(\xi)$, which are generally available in the literature, for example in [2].