Using the Residue Theorem

Considering that in the $R\to\infty$ limit the poles with residues $r_{k}(p,\nu)$ are all that exist strictly within the circuit, that the pole with residue $r_{0}(p,\nu)$ is the only one located over the circuit, and that the integral is defined as the Cauchy principal value at this pole, we can use the residue theorem to write for the integral

$$\lim_{R\to\infty} \oint_{C}f(p,\nu,\xi)\,d\xi = 2\pi\ima... ... r_{0}(p,\nu) + \sum_{k=1}^{\infty} r_{k}(p,\nu) \right].$$ (33)

On the other hand, as we saw above the integral vanishes in the $R\to\infty$ limit, and hence we have

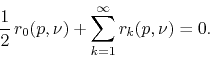$$\frac{1}{2}\, r_{0}(p,\nu) + \sum_{k=1}^{\infty} r_{k}(p,\nu) = 0.$$ (34)

We have therefore the following general result involving all these residues, substituting the values we calculated before for each one of them,

$$\frac{\Gamma(\nu+1)}{2^{p+1}\Gamma(\nu+p+1)} = \sum_{k=1}... ...+1}}\, \frac{J_{\nu+p}(\xi_{\nu k})}{J_{\nu+1}(\xi_{\nu k})}.$$ (35)

This is valid for any real value of $\nu\geq 0$ and for any real value of $p>0$.