Next: Proof of a General Up: On the Sums of Previous: Using the Residue Theorem
Up to this point ![]() could be any strictly positive real number. From now
on, however, we have to assume that
could be any strictly positive real number. From now
on, however, we have to assume that ![]() is a strictly positive integer. In order to further simplify the expression obtained above, in
general it will be necessary to write
is a strictly positive integer. In order to further simplify the expression obtained above, in
general it will be necessary to write
![]() in terms of
in terms of
![]() , which can be done using the recurrence formula
of the Bessel functions [6], so long as
, which can be done using the recurrence formula
of the Bessel functions [6], so long as ![]() is an integer. Let
us examine a few of the initial cases. For
is an integer. Let
us examine a few of the initial cases. For ![]() we have simply
we have simply
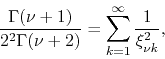 |
(36) |
so that the formula for the sum that corresponds to this case is
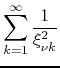 |
|||
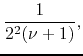 |
(37) |
were we used the properties of the gamma function, thus obtaining a
polynomial on ![]() in the denominator. In this way we obtain the first of
the known results, and this formula is therefore proven, being valid for
any non-negative real value of
in the denominator. In this way we obtain the first of
the known results, and this formula is therefore proven, being valid for
any non-negative real value of ![]() . For
. For ![]() we have
we have
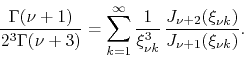 |
(38) |
In order to simplify this expression we write the recurrence formula as
| (39) |
where we exchanged ![]() for
for ![]() . Applying this for
. Applying this for
![]() and using once more the fact that
and using once more the fact that
![]() , we get
, we get
| (40) |
so that in this case we have
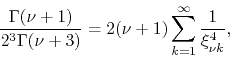 |
(41) |
from which it follows that the formula for the sum that corresponds to this case is
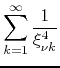 |
|||
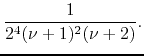 |
(42) |
We thus obtain the second known result, which is now proven, and which
also has a polynomial on ![]() in the denominator. The proof of the first
two formulas is therefore quite straightforward. In the
in the denominator. The proof of the first
two formulas is therefore quite straightforward. In the ![]() case,
however, something slightly different happens. In this case we have
case,
however, something slightly different happens. In this case we have
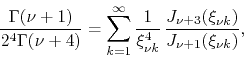 |
(43) |
and hence we must write one more version of the recurrence formula.
Exchanging ![]() for
for ![]() in the original formula, and applying at
in the original formula, and applying at
![]() , we obtain
, we obtain
| (44) |
Substituting in this the solution found for the previous case, which gives
us
![]() in terms of
in terms of
![]() , we get
, we get
![\begin{displaymath}
J_{\nu+3}(\xi_{\nu k})
=
\left[
\frac{2^{2}(\nu+1)(\nu+2)}{\xi_{\nu k}^{2}}
-
1
\right]
J_{\nu+1}(\xi_{\nu k}).
\end{displaymath}](img153.png) |
(45) |
In this way we get in this case the result
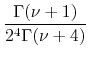 |
![$\displaystyle \sum_{k=1}^{\infty}
\frac{1}{\xi_{\nu k}^{4}}
\left[
\frac{2^{2}(\nu+1)(\nu+2)}{\xi_{\nu k}^{2}}
-
1
\right]$](img155.png) |
||
| (46) |
We see that in this case a linear combination of the sums of two different
powers of the zeros ![]() appears. Using the properties of the
gamma function and substituting the value obtained previously for
appears. Using the properties of the
gamma function and substituting the value obtained previously for
![]() , we get for
, we get for ![]()
| (47) |
The formula for the sum that corresponds to this case is therefore
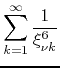 |
|||
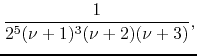 |
(48) |
where we once more have a polynomial on ![]() in the denominator. We thus
obtain the third of the known results, and the formula for
in the denominator. We thus
obtain the third of the known results, and the formula for ![]() is proven.
is proven.
It is clear that we can proceed in this way indefinitely, thus obtaining
the formulas for successive values of ![]() . In each case it is necessary to
first use the recurrence formula in order to write
. In each case it is necessary to
first use the recurrence formula in order to write
![]() in
terms of
in
terms of
![]() . In general the result will be a linear
combination of sums of several distinct inverse powers of
. In general the result will be a linear
combination of sums of several distinct inverse powers of ![]() .
At this point the use of the general formula in Eq. (35)
will produce an expression for the linear combination of the corresponding
sums
.
At this point the use of the general formula in Eq. (35)
will produce an expression for the linear combination of the corresponding
sums ![]() . Finally, it is necessary to solve the resulting
expression for the sum with the largest value of
. Finally, it is necessary to solve the resulting
expression for the sum with the largest value of ![]() so far, using for
this end the results obtained previously for the other sums. In this way
all the formulas for the sums
so far, using for
this end the results obtained previously for the other sums. In this way
all the formulas for the sums ![]() can be derived successively
by purely algebraic means, resulting every time in the ratio of two
polynomials, with the one in denominator completely factored.
can be derived successively
by purely algebraic means, resulting every time in the ratio of two
polynomials, with the one in denominator completely factored.