Next: Some Particular Cases Up: On the Sums of Previous: Proof of Some Known
It is possible to systematize the resolution process described above to
the point where a general formula for the linear combination of the sums
![]() can be written. This is based on a systematization of the
general formula for the ratio of Bessel functions, which is found to be
can be written. This is based on a systematization of the
general formula for the ratio of Bessel functions, which is found to be
where ![]() for odd
for odd ![]() and
and ![]() for even
for even ![]() , and
for which we will provide proof in what follows. The use of the general
formula in Eq. (35) then produces a corresponding general
formula for the linear combination of the sums
, and
for which we will provide proof in what follows. The use of the general
formula in Eq. (35) then produces a corresponding general
formula for the linear combination of the sums ![]() ,
,
Note that the left-hand side of this equation can be written as the
inverse of a polynomial on ![]() , with integer coefficients, with the
simple use of the properties of the gamma function. On the other hand, the
coefficients on the right-hand side can all be written as polynomials on
, with integer coefficients, with the
simple use of the properties of the gamma function. On the other hand, the
coefficients on the right-hand side can all be written as polynomials on
![]() , with integer coefficients, since we have for the arguments of the
two gamma functions, in the numerator and in the denominator,
, with integer coefficients, since we have for the arguments of the
two gamma functions, in the numerator and in the denominator,
| (51) |
where ![]() is an integer whose minimum value is
is an integer whose minimum value is ![]() for odd
for odd ![]() , and
, and
![]() for even
for even ![]() . It follows that, once the equation is solved for
. It follows that, once the equation is solved for
![]() , resulting in
, resulting in
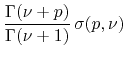 |
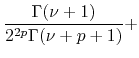 |
||
![$\displaystyle -
\sum_{q=1}^{q_{M}}
\frac{(-1)^{q}}{2^{2q}}\,
\frac{[(p-1)-q]!\;\Gamma(\nu+p-q)}{[(p-1)-2q]!\;q!\;\Gamma(\nu+q+1)}\,
\sigma(p-q,\nu),$](img173.png) |
(52) |
and assuming that the previous sums all have this same property, the
expression for this sum will have the form of the ratio of two polynomials
on ![]() , with integer coefficients. Hence, since we saw that this is
valid for the first three sums, by finite induction it is valid for all the sums.
, with integer coefficients. Hence, since we saw that this is
valid for the first three sums, by finite induction it is valid for all the sums.
This set of equations, taken for all strictly positive integer values of
![]() , forms an infinite linear system of equations in triangular form, that
can be solved iteratively in order to obtain closed forms for
, forms an infinite linear system of equations in triangular form, that
can be solved iteratively in order to obtain closed forms for
![]() in a purely algebraic way, in principle for arbitrary
integer values of
in a purely algebraic way, in principle for arbitrary
integer values of ![]() , although for large values of
, although for large values of ![]() the algebraic work
involved can be very large. However, it is straight, direct algebraic
work, well suited for a computer-algebra approach.
the algebraic work
involved can be very large. However, it is straight, direct algebraic
work, well suited for a computer-algebra approach.
We will now prove these two general formulas. Since the general formula in
Eq. (50) follows from the general formula in
Eq. (49), it suffices to prove the latter. We can do this by
finite induction. Since the upper limits of the summations involved depend
on the parity of ![]() , it is necessary to consider the two cases
separately. The first step is to verify that our general formula
reproduces the correct results for the first three cases, which we have
already derived individually. Applying the general formula in
Eq. (49) for
, it is necessary to consider the two cases
separately. The first step is to verify that our general formula
reproduces the correct results for the first three cases, which we have
already derived individually. Applying the general formula in
Eq. (49) for ![]() , in which case we have
, in which case we have ![]() , we obtain
at once
, we obtain
at once
| (53) |
which is obviously the correct result. Applying now the same general
formula for ![]() , for which we also have
, for which we also have ![]() , we get
, we get
| (54) |
which is also the correct result. Finally, applying the general formula
for ![]() , in which case we have
, in which case we have ![]() , we obtain
, we obtain
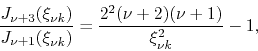 |
(55) |
which once more is the correct result. It suffices now to use the
recurrence formula of the Bessel functions to show that the formula for
![]() follows from the previous formulas, for
follows from the previous formulas, for ![]() e
e ![]() . We start with
the case in which
. We start with
the case in which ![]() is even, and writing explicitly the upper limits of
the sums, we have
is even, and writing explicitly the upper limits of
the sums, we have
Writing now the recurrence formula which gives the function
![]() in terms of
in terms of
![]() and
and
![]() , and substituting Eq. (56)
and (57), we get, after some manipulation of the indices of the
sums,
, and substituting Eq. (56)
and (57), we get, after some manipulation of the indices of the
sums,
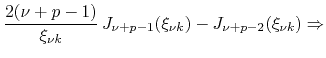 |
|||
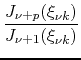 |
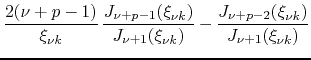 |
||
![$\displaystyle \sum_{q=0}^{(p-2)/2}
(-1)^{q}\,
\frac
{[(p-1)-q]!\;\Gamma(\nu+p-q)}
{[(p-1)-2q]!\;q!\;\Gamma(\nu+q+1)}
\times$](img191.png) |
|||
![$\displaystyle \hspace{3em}
\times
\frac
{(\nu+p-1)[(p-1)-2q]+q(\nu+q)}
{[(p-1)-q][\nu+(p-1)-q]}
\left(\frac{2}{\xi_{\nu k}}\right)^{(p-1)-2q}.$](img192.png) |
(58) |
It is easy to verify that we have for the second fraction in this sum,
| (59) |
We therefore conclude that
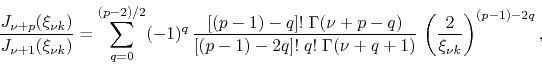 |
(60) |
thus proving the general formula for even ![]() . For odd
. For odd ![]() , once more
writing explicitly the upper limit of the sums, we start from
, once more
writing explicitly the upper limit of the sums, we start from
Writing once again the recurrence formula which gives
![]() in terms of
in terms of
![]() and
and
![]() , and substituting Eq. (61) and (62), we get,
after some similar manipulation of the indices of the sums,
, and substituting Eq. (61) and (62), we get,
after some similar manipulation of the indices of the sums,
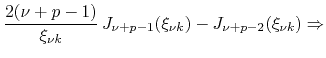 |
|||
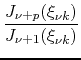 |
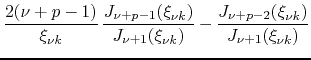 |
||
![$\displaystyle \sum_{q=0}^{(p-3)/2}
(-1)^{q}\,
\frac
{[(p-1)-q]!\;\Gamma(\nu+p-q)}
{[(p-1)-2q]!\;q!\;\Gamma(\nu+q+1)}
\times$](img197.png) |
|||
![$\displaystyle \hspace{3em}
\times
\frac
{(\nu+p-1)[(p-1)-2q]+q(\nu+q)}
{[(p-1)-q][\nu+(p-1)-q]}
\left(\frac{2}{\xi_{\nu k}}\right)^{(p-1)-2q}$](img198.png) |
|||
| (63) |
The second fraction within the last summation, which does not involve
factorials, is the same as before, and therefore is equal to ![]() . It
follows that we have
. It
follows that we have
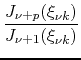 |
![$\displaystyle \sum_{q=0}^{(p-3)/2}
(-1)^{q}\,
\frac
{[(p-1)-q]!\;\Gamma(\nu+p-q...
...p-1)-2q]!\;q!\;\Gamma(\nu+q+1)}\,
\left(\frac{2}{\xi_{\nu k}}\right)^{(p-1)-2q}$](img200.png) |
||
| (64) |
It is not difficult to verify that the additional term that we have here
is in fact equal to the argument of the summation in the case ![]() ,
so that we may merge it with the summation and this obtain
,
so that we may merge it with the summation and this obtain
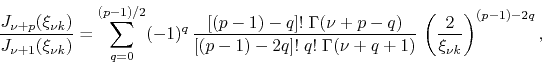 |
(65) |
thus proving the general formula in this case. This completes the proof of
the general formula in Eq. (49), from which follows the
general formula in Eq. (50) for the linear combination of the
sums ![]() , which is therefore proven as well.
, which is therefore proven as well.