Next: Acknowledgements Up: On the Sums of Previous: Proof of a General
We may now use the general formula in Eq. (50) for
![]() in order to write explicitly a few cases which are not
found in the current literature. With a little help from the free-software
algebraic manipulation program maxima, we get the following two
results, thus completing the sequence of known results up to
in order to write explicitly a few cases which are not
found in the current literature. With a little help from the free-software
algebraic manipulation program maxima, we get the following two
results, thus completing the sequence of known results up to ![]() ,
,
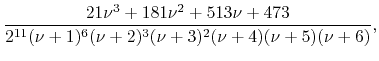 |
(66) | ||
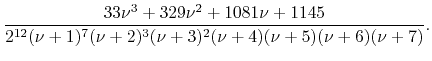 |
(67) |
We now point out that our results for ![]() are valid for all
real values of
are valid for all
real values of ![]() , not just for the integers. Therefore, exchanging
, not just for the integers. Therefore, exchanging
![]() for
for ![]() we may obtain formulas that are valid for the zeros of
the regular spherical Bessel functions
we may obtain formulas that are valid for the zeros of
the regular spherical Bessel functions ![]() , since we have the
well-known relation
, since we have the
well-known relation
| (68) |
between these two families of functions. In particular, using the value
![]() we obtain the results for
we obtain the results for ![]() , whose zeros are given by
, whose zeros are given by
![]() , since this particular function is proportional to
, since this particular function is proportional to
![]() [7]. In this way we obtain a direct relation
between our results and the Riemann zeta function, for certain real
integer arguments of
[7]. In this way we obtain a direct relation
between our results and the Riemann zeta function, for certain real
integer arguments of ![]() . In fact, we have
. In fact, we have
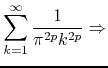 |
|||
| (69) |
Using the formulas we obtained here for ![]() in the case
in the case
![]() , we obtain for example the values
, we obtain for example the values
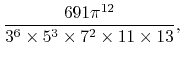 |
(70) | ||
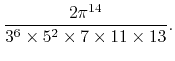 |
(71) |
Finally, using our general formula for the case ![]() and solving for
and solving for
![]() , once more with some help from the free-software program
maxima, we obtain
, once more with some help from the free-software program
maxima, we obtain
| (72) |
where the two polynomials are given by
| (73) | |||
| (74) |
Up to the case ![]() it is possible and in fact fairly easy to verify the
resulting formulas numerically with good precision, with the use of
standard computational facilities. However, in this
it is possible and in fact fairly easy to verify the
resulting formulas numerically with good precision, with the use of
standard computational facilities. However, in this ![]() case it is just
too difficult to verify this formula by numerical means, except for
case it is just
too difficult to verify this formula by numerical means, except for
![]() , using the usual double-precision floating-point arithmetic. In
order to do this one would have to use quadruple precision or better
numerical arithmetic. The difficulty seems to lie in the direct numerical
calculation of the sum
, using the usual double-precision floating-point arithmetic. In
order to do this one would have to use quadruple precision or better
numerical arithmetic. The difficulty seems to lie in the direct numerical
calculation of the sum ![]() , not in the evaluation of the ratio
of polynomials. Hence, the results discussed here acquire an algorithmic,
numerical significance, enabling one to easily calculate the values of the
sums.
, not in the evaluation of the ratio
of polynomials. Hence, the results discussed here acquire an algorithmic,
numerical significance, enabling one to easily calculate the values of the
sums.