- ...
surgiram

- Vários livros que discutem estes formalismos podem ser
encontrados na literatura
[2,3,4,5,6,7].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... acima

- Um
vórtice é o análogo, em
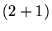 dimensões, do monopólo
magnético em
dimensões, do monopólo
magnético em 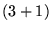 dimensões [35]. Monopólos
magnéticos passaram a ser incorporados à eletrodinâmica
clássica de Maxwell a partir de estudos feitos por Dirac
[36] em meados de 1930 e possibilitaram uma explicação,
a nível quântico, da quantização da carga
elétrica. Mais tarde 't Hooft incorporou esta análise às teorias
de Yang-Mills [37].
dimensões [35]. Monopólos
magnéticos passaram a ser incorporados à eletrodinâmica
clássica de Maxwell a partir de estudos feitos por Dirac
[36] em meados de 1930 e possibilitaram uma explicação,
a nível quântico, da quantização da carga
elétrica. Mais tarde 't Hooft incorporou esta análise às teorias
de Yang-Mills [37].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... enfoques

- Veja, por exemplo, a
referência [5].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
temperaturas
- Este limite existe ainda na fase de simetria
quebrada. Por exemplo, para
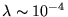 , a temperatura
crítica
, a temperatura
crítica 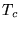 na qual a simetria é restaurada é da ordem de
na qual a simetria é restaurada é da ordem de
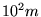 [39,7] e portanto existe uma temperatura
[39,7] e portanto existe uma temperatura 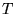 inferior a
inferior a 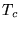 e ainda suficientemente grande para que possa ser
considerada a expansão de altas temperaturas.
e ainda suficientemente grande para que possa ser
considerada a expansão de altas temperaturas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
paridade
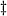
- Note que, em
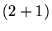 dimensões o traço de
três matrizes
dimensões o traço de
três matrizes 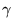 deixa de ser nulo, como acontece em
deixa de ser nulo, como acontece em 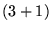 dimensões e passa a ser proporcional a
dimensões e passa a ser proporcional a
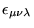 . Com isso, no caso de férmions massivos, correções
radiativas são geradas para o termo de Chern-Simons,
independentemente dele existir ou não na aproximação de
árvore.
. Com isso, no caso de férmions massivos, correções
radiativas são geradas para o termo de Chern-Simons,
independentemente dele existir ou não na aproximação de
árvore.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... constante

- A álgebra de operadores
nestes espaços foi extensivamente estudada, sendo conhecidas
muitas propriedades [23,43].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...c\ ao
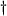
- Note que, devido à definição do
produto-estrela, Eq. (4.12), os termos em
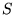 contendo
interação entre campos passam a conter um número ilimitado de
derivadas, o que indica que a teoria assim descrita é não-local.
contendo
interação entre campos passam a conter um número ilimitado de
derivadas, o que indica que a teoria assim descrita é não-local.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...eq.14)
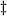
- Implicitamente o que está sendo
considerado é que a medida funcional não se altera com a
introdução do produto Moyal. A referência [44]
apresenta uma boa discussão sobre esta questão.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
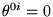
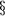
- A restrição da não comutatividade
somente às componentes espaciais de
 é assumida para
evitarmos complicações associadas com unitariedade e/ou
causalidade [45].
é assumida para
evitarmos complicações associadas com unitariedade e/ou
causalidade [45].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.