Modelo de Chern-Simons

Antes de discutirmos teorias de Chern-Simons propriamente ditas, vale a pena relembrar alguns fatos de teorias de calibre em geral. Considere, assim, uma teoria representando férmions livres em uma dimensão $D$ qualquer. A lagrangiana deste modelo é a de Dirac, expressa por:

$${\cal L}^{(0)}_{D} = \bar{\psi}(x) (i \gamma^{\mu} \partial_{\mu} - m) \psi(x).$$ (2.33)

Esta lagrangiana é invariante sob uma transformação de calibre global, ou seja,

$$\delta \psi = i \alpha \psi, \qquad \delta \bar{\psi} = - i \alpha \bar{\psi},$$ (2.34)

onde $\alpha=$ constante é o parâmetro da transformação. Podemos promover esta invariância de calibre global a uma invariância de calibre local (com $\alpha \equiv \alpha(x)$), através de um campo de calibre auxiliar $A_{\mu }$, que se transforma como:

$$\delta A_{\mu} = \partial_{\mu} \alpha.$$ (2.35)

Incluímos este novo campo na teoria de forma a preservar a sua invariância de calibre local, através de uma derivada covariante, ou seja,

$$D_{\mu} \equiv \partial_{\mu} - i e A_{\mu},$$ (2.36)

de tal forma que a nova teoria agora é dada por

$${\cal L}_{D} = \bar{\psi}(x) (i \gamma^{\mu} D_{\mu} - m) \psi(x).$$ (2.37)

Podemos ainda dar uma dinâmica para este campo de calibre. A forma usual de ser fazer isso é obrigando-o a obedecer a dinâmica imposta pelas equações de Maxwell. Neste caso, a sua lagrangiana é dada por:

$${\cal L}_M = - \frac{1}{4} F_{\mu \nu} F^{\mu \nu},$$ (2.38)

e a lagrangiana total da teoria torna-se:

$${\cal L}_T = {\cal L}_D+ {\cal L}_M.$$ (2.39)

A teoria descrita por ${\cal L}_T$ é a eletrodinâmica.

Porém no plano, isto é, em $(2+1)$ dimensões, existe um outro possível termo quadrático no campo de calibre que, assim como o termo de Maxwell, também respeita invariância de Lorentz e de calibre. Este termo é dado pela Eq. (1.1), ou seja,

$${\cal L}_{CS} = \frac{\kappa}{2} \epsilon_{\mu \nu \lambda} A^{\mu} \partial^{\nu} A^{\lambda}.$$ (2.40)

A teoria descrita pela Eq. (2.40) é conhecida como teoria de Chern-Simons [9] e tem características próprias [34], como veremos a seguir. Em primeiro lugar, ${\cal L}_{CS}$ é de primeira ordem nas derivadas espaço-temporais. Desta forma, é de se esperar que a dinâmica do modelo tenha uma estrutura consideravelmente diferente da imposta pela lagrangiana de Maxwell. De fato, ao calcularmos as equações de Euler-Lagrange, chegamos a:

$$F_{\mu \nu} = 0,$$ (2.41)

ou seja, a teoria admite somente soluções com configurações triviais de campo, se não estiver acoplada a algum tipo de matéria ou, pelo menos, que tenha um novo termo cinético, modificando as suas equações de movimento. Neste texto apresentaremos algumas possibilidades: acoplamento com uma corrente $J_{\mu}$ e com um campo de Higgs, e inserção de um termo de Maxwell.

Começando por acoplar ao campo de Chern-Simons uma densidade de corrente $J_{\mu}$, temos:

$${\cal L} \equiv {\cal L}_{CS} - A_{\mu} J^{\mu}.$$ (2.42)

Neste caso a equação de movimento torna-se:

$$J^{\mu} = \frac{\kappa}{4} \epsilon^{\mu \nu \lambda} F_{\nu \lambda},$$ (2.43)

ou, em termos de componentes,

$$\rho = \kappa B,$$

$$J^i = \kappa \epsilon^{i j} E_j.$$ (2.44)

onde $B$ e $\vec{E}$ representam os campos magnético e elétrico respectivamente. Aqui notamos um resultado interessante: o acoplamento de Chern-Simons pode ser visto como um vínculo ao sistema, ou seja, ele associa um fluxo de campo magnético $B$ à densidade de corrente $\rho$. Sempre que houver um, o outro deverá aparecer também. A referência [34] traz uma boa discussão das consequências deste acoplamento.

Uma segunda possibilidade seria unir ${\cal L}_M$, Eq. (1.2), a ${\cal L}_{CS}$. Neste caso a equação de movimento torna-se:

$$\partial_{\mu} F^{\mu \nu} + \frac{\kappa}{2} \epsilon^{\nu \alpha \beta } F_{\alpha \beta} = 0.$$ (2.45)

Em termos do campo de Maxwell, podemos interpretar a introdução do termo de Chern-Simons, ${\cal L}_{CS}$, como um mecanismo para geração de massa para o campo $A_{\mu }$ que não depende da escolha de calibre. Existem duas maneiras de entender melhor esta afirmação. Uma é olhar diretamente para a equação de movimento acima, através do uso de um campo auxiliar $\tilde{F}^{\mu} \equiv \epsilon^{\mu \nu \lambda} F_{\nu \lambda}$. Ao invés disso, já pensando na teoria quântica, vamos examinar o propagador do modelo, expresso, no espaço euclidiano, por:

$$D_{\mu \nu} (p) = \frac{1}{p^2 + \kappa^2} \left[ \delta_{\m... ..._{\lambda}}{p^2}\right] + \xi \frac{p_{\mu} p_{\nu}}{(p^2)^2},$$ (2.46)

onde estamos considerando um calibre covariante tipo Lorentz e $p \equiv (2 \pi n T, \vec{p})$. Podemos identificar a massa do campo de calibre, $m_{A_{\mu}}$, como sendo o pólo do propagador, ou seja,

$$m_{A_{\mu}} = \kappa.$$ (2.47)

Neste contexto, vale lembrar que existe um outro mecanismo de geração de massa para o campo $A_{\mu }$, conhecido como Mecanismo de Higgs, associado com a quebra espontânea de simetria. Como veremos, juntando estas duas possibilidades, obtemos uma teoria com características próprias. Considerando este caso, temos a seguinte lagrangiana:

$${\cal L}_{MCSH} \equiv {\cal L}_M + {\cal L}_{CS} + {\cal L}_H,$$ (2.48)

onde ${\cal L}_H$ é expresso pela Eq. (1.3), ou seja,

$${\cal L}_H = \vert D_{\mu} \Phi\vert^2 - \frac{\lambda}{4} (\vert\Phi\vert^2 - v^2)^2.$$ (2.49)

Podemos, ainda, expandir o campo escalar em torno do seu valor esperado no vácuo, $\langle\vert\Phi\vert\rangle=v$, como $\Phi = v + \frac{1}{\sqrt{2}}(\sigma + i \chi)$. Fazendo isso e considerando o calibre $R_{\xi}$, ou seja,

$${\cal L}_{FG} = - \frac{1}{2 \xi} \left( \partial_{\mu} A^{\mu} + \xi e \sqrt{2} v \chi \right)^2,$$ (2.50)

a lagrangiana ${\cal L}_{MCSH}$ torna-se:

$${\cal L}_{MCSH} = - \frac{1}{4} F_{\mu \nu} F^{\mu \nu} + \frac{\kappa}{2} \epsilon... ...da} + \frac{m^2}{2} A_{\mu}A^{\mu} - \frac{1}{2 \xi} (\partial_{\mu} A^{\mu})^2$$

$$+ \frac{1}{2} \partial_{\mu} \sigma \partial^{\mu} \sigma - \frac{1... ...c{1}{2} \partial_{\mu} \chi \partial^{\mu} \chi - \frac{1}{2} m_{\chi}^2 \chi^2$$

$$- e \sigma \, {\buildrel\,\leftrightarrow\over{\partial^{\mu}}\!\!}... ..._{\mu} + \frac{e^2}{2} (\sigma^2 + \chi^2 + 2 \sqrt{2} v \sigma) A_{\mu}A^{\mu}$$

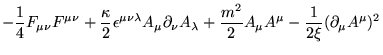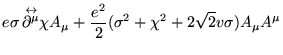$$- \frac{\lambda}{2 \sqrt{2}} v \sigma (\sigma^2 + \chi^2) - \frac{\lambda}{16}(\sigma^2 + \chi^2)^2.$$ (2.51)

Com esta escolha de calibre, o termo bilinear $\sqrt{2} v \chi \partial_{\mu} A^{\mu}$, que mistura o bóson de Goldstone ao campo de calibre, desaparece. Estamos também definindo as seguintes massas:

$$m^2= 2 e^2 v^2, \qquad m_{\sigma}^2= \lambda v^2, \qquad m_{\chi}^2= \xi m^2.$$ (2.52)

O propagador do campo $A_{\mu }$ é dado por [25]:

$$D_{\mu \nu} (p) = \frac{1}{(p^2 + m^2_+)(p^2 + m^2_-)}$$

$$\times \left[ \delta_{\mu \nu} - p_{\mu}p_{\nu} \frac{(1-\xi)(p^2 + m^2)... ...appa^2}{p^2 + \xi m^2} - \kappa \epsilon_{\mu \nu \lambda} p_{\lambda} \right],$$ (2.53)

com

$$m^2_{\pm} = \frac{\kappa^2 + 2 m^2 \pm \vert\kappa\vert\sqrt{\kappa^2 + 4 m^2}}{2}.$$ (2.54)

A teoria descrita por ${\cal L}_{MCSH}$ possui muitas propriedades interessantes, algumas delas completamente diferentes das existentes no acoplamento do campo de Maxwell com o campo de Higgs. Olhando diretamente para o propagador (2.53), por exemplo, podemos notar a presença agora de duas massas físicas, $m\pm$. Este resultado era, de certa forma, esperado, uma vez que introduzimos na teoria dois mecanismos de geração de massa para o campo de calibre: a massa topológica $\kappa$ e a massa gerada via mecanismo de Higgs. Algumas questões surgem devido a esta propriedade, como por exemplo, como fazer a análise dos processos de blindagem, já que as massas físicas com eles associadas podem ser obtidas dos pólos do propagador. Deixaremos a análise deste ponto para ser explorada mais profundamente no próximo capítulo.

Outra característica está associada com a existência de soluções estáveis com energia finita. Em $(2+1)$ dimensões, sabe-se que as teorias de campo de Maxwell acoplado com campo de Higgs, tanto abelianas [10] quanto não abelianas [11], não admitem soluções tipo vórtice eletricamente carregado com o comportamento acima. Já a inserção, nestes modelos, de um termo de Chern-Simons altera completamente esta estrutura, possibilitando a existências de tais soluções [12,13].