Formalismo de Tempo Imaginário

O formalismo de tempo imaginário consiste em uma generalização da teoria quântica de campos usual, na qual a variável temporal é rodada no plano complexo de tal forma a estar no eixo imaginário negativo. Com isso, o tempo passa a ser interpretado como temperatura, fazendo com que o formalismo assim desenvolvido seja mais apropriado para descrever sistemas estatísticos em equilíbrio. A seguir, iremos estudar detalhadamente estas afirmações.

Considere inicialmente um sistema mecânico descrito classicamente pela hamiltoniana $H$, independente do tempo. Na abordagem da mecânica estatística, a física deste sistema é obtida através do cálculo da matriz densidade $\rho\equiv \rho(\beta)$, definida em um particular ensemble através da função $K$, como:

$$\rho(\beta) \equiv e^{- \beta K},$$ (2.1)

onde $\beta=1/(k T)$, com $T$ sendo a temperatura do sistema e $k$ a constante de Boltzmann. Por exemplo, para o ensemble canônico, $K=H$. Já no ensemble grande-canônico, $K=H - \mu N$, onde $N$ é o número de partículas do sistema e $\mu$ o seu potencial químico [30]. Da expressão acima, vemos que $\rho(\beta)$ satisfaz a equação de Bloch, expressa por:

$$- \frac{\partial \rho}{\partial \beta} = K \rho.$$ (2.2)

A partir de $\rho$ podemos obter a função de partição $Z$ que contém toda a informação sobre o sistema estatístico, como sendo:

$$Z = \mbox{Tr} \rho.$$ (2.3)

Resolver o sistema significa determinar o traço acima, ou seja, somar $\rho$ sobre todo o espectro de energias do sistema. O problema é que, na maioria dos casos, este espectro não é conhecido de maneira exata. Podemos então efetuar um cálculo perturbativo para obter $Z$. Consideramos que $K$ possa ser escrito como $K = K_0 + K_I$, onde $K_0$ é tal que $Z(K_0)$ é conhecida e $K_I$ é uma perturbação imposta ao sistema. Com isso, desenvolvemos uma teoria de perturbação de $Z$ em torno de $Z(K_0)$.

Uma consequência destas hipóteses a respeito do sistema estatístico é que podemos definir uma nova função $S\equiv S(\beta)$, através de:

$$e^{-\beta K} = \rho \equiv e^{- \beta K_0} S(\beta),$$ (2.4)

de tal maneira que a equação de Bloch, expressa em termos de $S$, torna-se:

$$-\frac{\partial S(\beta)}{\partial \beta} = K_I S(\beta).$$ (2.5)

Como veremos a seguir, a expressão acima é similar à derivada com relação ao tempo do operador de evolução temporal $\hat{\cal U}(t,t')$ da teoria quântica, ou seja, $S(\beta)$ é qualitativamente semelhante a $\hat{\cal U}(t,t')$ e esta será a essência da formulação da Teoria Quântica de Campos à Temperatura Finita.

Para entender melhor o que acabamos de ressaltar, vamos considerar um sistema quântico qualquer. Neste caso, os observáveis são expressos através de operadores em um espaço de Hilbert, com características que dependem da representação escolhida. Na representação de Schrödinger, por exemplo, eles são independentes do tempo. Já nas representações de Heisenberg e de interação eles são expressos, respectivamente, por:

$$\hat{\cal O}_H(t) = e^{i \hat{H} t/\hbar} \, \hat{\cal O}_S \, e^{- i \hat{H} t/\hbar},$$ (2.6)

e

$$\hat{\cal O}_I(t) = e^{i \hat{H}_0 t/\hbar} \, \hat{\cal O}_S \, e^{- i \hat{H}_0 t/\hbar},$$ (2.7)

onde $\hat{\cal O}_S$ é o operador na representação de Schrödinger. Como é claro da notação empregada, estamos considerando que a hamiltoniana do sistema possa ser decomposta como $H= H_0 + H_I$. A relação entre $\hat{\cal O}_H(t)$ e $\hat{\cal O}_I(t)$ pode ser escrita com o uso do operador de evolução temporal $\hat{\cal U}(t_1,t_2)$, como:

$$\hat{\cal O}_H(t) = \hat{\cal U}(0,t) \, \hat{\cal O}_I(t) \, \hat{\cal U}(t,0).$$ (2.8)

Na equação acima estamos definindo $\hat{\cal U}(t_1,t_2)$ como sendo:

$$\hat{\cal U}(t_1,t_2) =e^{i \hat{H}_0 t_1/\hbar} \, e^{-i \hat{H} (t_1 - t_2)/\hbar} \, e^{- i \hat{H}_0 t_2/\hbar},$$ (2.9)

satisfazendo a seguinte equação de movimento:

$$i \hbar \frac{\partial}{\partial t}\hat{\cal U}(t,t') = \hat{H}_I (t)\hat{\cal U}(t,t'),$$ (2.10)

onde $\hat{H}_I(t)$ e é o operador $H_I$ na representação de interação. Agora, ao compararmos as Eqs. (2.5) e (2.10) podemos interpretar a primeira delas como sendo a equação de movimento para o operador $\hat{S}$ em uma representação ``modificada''de interação. Para isso, basta realizarmos uma rotação do tempo para o eixo imaginário negativo no sentido horário, $t \rightarrow - i\hbar \beta$, e mapearmos $\hat{H} \rightarrow \hat{K}$. Com estas mudanças, podemos estudar a Mecânica Estatística na abordagem quântica e esta é a idéia básica contida no formalismo de tempo imaginário. Poderíamos começar a apresentação a partir deste ponto, simplesmente definindo uma nova representação de interação a partir de:

$$\hat{\cal O}_K(\tau) = e^{\hat{K}_0 \tau} \, \hat{\cal O}_S \, e^{- \hat{K}_0 \tau}.$$ (2.11)

Como já foi dito, o ponto de partida deste formalismo é a generalização proposta na Eq. (2.11). Nesta linha, definimos também a representação ``modificada'' de Heisenberg como:

$$\hat{\cal O}_H(\tau) \equiv e^{\hat{K}\tau} \, \hat{\cal O}_S \, e^{- \hat{K} \tau}$$

$$= \hat{\cal U}(0,\tau) \, \hat{\cal O}_K (\tau) \, \hat{\cal U} (\tau,0),$$ (2.12)

onde o operador de evolução temporal (modificado) é expresso por:

$$\hat{\cal U}(\tau_1,\tau_2) \equiv e^{\hat{K}_0 \tau_1} e^{- \hat{K} (\tau_1 - \tau_2)} e^{- \hat{K}_0 \tau_2},$$ (2.13)

e obedece à seguinte evolução temporal:

$$- \frac{\partial \hat{\cal U}(\tau,\tau') }{ \partial \tau} = \hat{K}_I(\tau) \hat{\cal U}(\tau,\tau').$$ (2.14)

O operador densidade neste novo formalismo passa a ser também uma generalização da Eq. (2.1), expressa por:

$$\hat{\rho}(\beta) \equiv e^{- \hat{K} \beta} = e^{- \hat{K}_0 \beta} \hat{\cal U} (\beta,0),$$ (2.15)

de tal forma que os observáveis da teoria passam a ser escritos como médias estatísticas nos ensembles especificados por $\hat{\rho}$, ou seja:

$$\langle{\cal O}\rangle \equiv \langle{\cal O}\rangle_{\beta}$$

$$= \frac{\mbox{Tr} \, \hat{\rho} \hat{\cal O}} {\mbox{Tr} \hat{\rho} } =\frac{\mbox{Tr}\, \hat{\rho} \hat{\cal O}} {Z },$$ (2.16)

onde $Z$ é a função de partição do sistema. A partir desta formulação, podemos interpretar a TQC a $T \ne 0$ como sendo o caso usual, mas com os observáveis sendo calculados como médias nos ensembles expressos por $\rho$ e $K$, ao invés de médias nos estados de vácuo. Novamente, de maneira análoga ao caso clássico, encontrar $Z$ significa calcular o traço da matriz densidade. Quanticamente esta operação é realizada sobre todos os autoestados de $\hat{H}$, que na maioria dos casos não são conhecidos de maneira exata. Faz-se necessário, uma vez mais, o uso de técnicas perturbativas.

Também podemos obter, em analogia ao formalismo usual, os mesmos resultados utilizando o método de integração funcional. Somente para ressaltar com um novo enfoque os principais conceitos envolvidos até aqui, vamos apresentar a seguir esta análise. Considere a função de partição da Mecânica Estatística, expressa a partir da função densidade como:

$$Z(\beta) = \mbox{Tr} \, \hat{\rho}(\beta) = \mbox{Tr} \, e^{- \beta \hat{H}}.$$ (2.17)

Por simplicidade, estamos considerando o ensemble canônico, onde $K=H$. Neste caso, a operação de traço deve ser calculada em uma base completa qualquer. Normalmente, considera-se esta como sendo o conjunto completo de autovetores de $\hat{H}$. Ao invés disso, vamos considerar o conjunto completo de autovetores do operador de campo $\hat{\phi}$ (vale salientar que, porque estamos interessados em analisar apenas aspectos gerais do formalismo, consideraremos o caso bosônico; sempre que o comportamento difira qualitativamente para o caso fermiônico, iremos ressaltar). Obtemos assim:

$$Z(\beta)= \int \mbox{d} \phi \langle\phi\vert \hat{\rho}(\beta) \vert\phi \rangle.$$ (2.18)

Novamente aqui podemos facilmente identificar $\hat{\rho}(\beta)$ como sendo um operador de evolução temporal para tempos imaginários. Em outras palavras, existe uma estrutura similar entre $Z(\beta)$ e a amplitude de transição da TQC usual [31]. Assim, se fizermos a generalização do operador evolução temporal proposta na Eq. (2.13) e seguirmos os passos da integração funcional chegaremos a [5,6]:

$$Z(\beta) = \int {\cal D} \phi e^{- \int_0^{\beta} d \tau \int d^3 x {\cal L}_E},$$ (2.19)

onde ${\cal L}_E$ é a densidade de lagrangiana associada com ${\cal H}$, no espaço euclidiano. A partir da Eq. (2.19), podemos expressar a média estatística (2.16) em termos de uma integração funcional. Assim, a função de partição $Z$ e consequentemente quaisquer observáveis estatísticos, como por exemplo pressão e número médio de partículas, podem ser calculados, senão de forma exata, pelo menos perturbativamente com o uso de técnicas similares às desenvolvidas nos métodos tradicionais. Podemos ainda obter as funções de correlação de maneira análoga às funções de Green da TQC. Para isso, basta usarmos a definição do funcional gerador da funções de Green da teoria, neste caso expresso por:

$$Z(\beta; j) \equiv \int {\cal D} \phi e^{ - \int_0^{\beta} d... ... \int d^3 x \left[{\cal L}_E - j(\vec{x}, \tau) \phi \right]},$$ (2.20)

de tal forma que a função de Green ${\cal G} (\tau_1, \tau_2)$, pode ser obtida como sendo:

$$\left. \frac{1}{Z(\beta)} \frac{\delta^2 Z(\beta; j)}{\delta j(\tau_1)\delta j(\tau_2)} \right\vert _{j=0} = \frac{1}{Z(\beta)} \int {\cal D} \, \phi \, \phi_{\tau_1} \phi_{\tau_2} \,e^{- S_E (\beta)}$$

$$\equiv {\cal G} (\tau_1, \tau_2).$$ (2.21)

onde por simplicidade estamos suprimindo a dependência em $\vec{x}$ das funções acima. Também definimos a ação $S_E(\beta)$ como sendo:

$$S_E(\beta) \equiv \int_0^{\beta} d \tau \int d^3 x {\cal L}_E.$$ (2.22)

Nesta linha muitos resultados da abordagem usual de TQC para o cálculo de diagramas de Feynman podem ser utilizados a $T \ne 0$. Alguns exemplos são o teorema de Wick e o cancelamento de diagramas desconexos [32]. A principal diferença aparece no fato de que nas integrais temporais para $T \ne 0$ o tempo é considerado num intervalo finito ao invés de variar de $-\infty$ a $+\infty$, como na abordagem usual. Uma consequência direta deste fato é que na transformada de Fourier de ${\cal G}$ as frequências associadas com o tempo finito são múltiplos inteiros de $\frac{\pi}{\beta}$. Mais especificamente, através de um cálculo direto [7], obtem-se que, para bósons, elas são dadas por:

$$w_n= \frac{2 \pi n}{\beta},$$ (2.23)

e para férmions:

$$w_n= \frac{(2n+1) \pi}{\beta},$$ (2.24)

que são conhecidas como as frequências de Matsubara [32,33]. Pode-se ainda demonstrar que, no caso bosônico, as variáveis de campo satisfazem condições de contorno periódicas com período $\beta$ na componente temporal e no caso fermiônico, antiperiódicas [7]. Em resumo, para uma análise perturbativa no formalismo de tempo imaginário, podemos utilizar as mesmas técnicas desenvolvidadas na TQC usual. Os vértices da teoria não se alteram; já para os propagadores, devemos considerar as componentes temporais dos quadri-momentos como sendo iguais a $w_n$.

Como um exemplo, considere a teoria $\phi^4$, expressa pela seguinte densidade de lagrangiana no espaço de Minkowski:

$${\cal L} = \frac{1}{2} \partial_{\mu} \phi \partial^{\mu} \phi - \frac{m^2}{2} \phi^2 - \frac{\lambda}{4!}\phi^4.$$ (2.25)

O propagador do campo $\phi$ é dado, no espaço euclidiano, por:

$$\Delta(k) = \frac{1}{k_0^2 + \vec{k}^2 + m^2} \equiv \frac{1}{w_n^2 + \vec{k}^2 + m^2},$$ (2.26)

com $w_n$ sendo as frequências de Matsubara, neste caso expressas pela Eq. (2.23). Já os vértices da teoria são os usuais, ou seja,

$$\mbox{v\'ertice quadrilinear} \rightarrow \frac{\lambda}{4!}.$$ (2.27)

A correção de massa a um laço é escrita como:

$$- \Delta m^2 = -\frac{\lambda}{2 \beta} \sum_n \int \frac{d^3 k}{(2 \pi)^3} \frac{1}{k_0^2 + \vec{k}^2 + m^2}$$

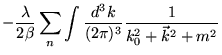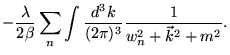$$\equiv -\frac{\lambda}{2 \beta}\sum_n \int \frac{d^3 k}{(2 \pi)^3} \frac{1}{w_n^2 + \vec{k}^2 + m^2}.$$ (2.28)

Note que, uma vez que as energias assumem valores específicos neste formalismo, dados pelas Eqs. (2.23) e (2.24), estamos utilizando o seguinte mapeamento para as variáveis de integração

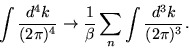$$\int \frac{d^4 k}{(2 \pi)^4} \rightarrow \frac{1}{\beta} \sum_n\int \frac{d^3 k}{(2 \pi)^3}.$$ (2.29)

As somas envolvidas no cálculo acima podem ser avaliadas sem dificuldades [5,6]. Já as integrais restantes nas componentes espaciais são mais complicadas e em geral requerem o uso de aproximações, como por exemplo os limites de alta e baixa temperaturas. Nos capítulos seguintes apresentaremos em detalhes alguns destes cálculos. Assim, neste exemplo, para o termo dependente da temperatura, obtemos [7]:

$$\Delta m_T^2 = \frac{\lambda}{24 \beta^2} + {\cal O}(\beta m).$$ (2.30)

Podemos ainda calcular observáveis termodinâmicos da teoria. Neste caso, precisamos determinar a função de partição $Z$. Novamente, em uma teoria interagente, este cálculo somente é possível perturbativamente. Assim temos:

$$Z = \int {\cal D} \phi e^{- S^0_E} e^{- S^I_E}$$

$$= \int {\cal D} \phi e^{- S^0_E} \sum_{l=0}^{\infty}\frac{1}{l!} (S^I_E)^l$$

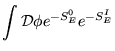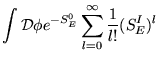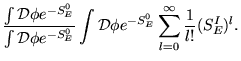$$= \frac{\int {\cal D} \phi e^{- S^0_E}}{\int {\cal D} \phi e^{- S^0_E}} \int {\cal D} \phi e^{- S^0_E} \sum_{l=0}^{\infty}\frac{1}{l!} (S^I_E)^l.$$ (2.31)

No cálculo que segue a partir deste ponto usamos, de maneira análoga à TQC sem incluir temperatura, a técnica diagramática para obter $\ln{Z}$ ordem a ordem na constante de acoplamento, ou seja,

$$\ln{Z} = \ln\left[ {\int {\cal D} \phi e^{- S^0_E}}\right] + \ln \left[\fr... ...\sum_{l=0}^{\infty}\frac{1}{l!} (S_I)^l}{\int {\cal D} \phi e^{- S^0_E}}\right]$$

$$\equiv \ln{Z_0} + \ln\left[{1 + \sum_{l=0}^{\infty}\frac{1}{l!} \langle(S_I)^l\rangle_{(0, \beta)}}\right],$$ (2.32)

onde o índice $(0,\beta)$ aparecendo em $\langle(S_I)^l\rangle$ indica que devemos considerar as médias com relação ao ensemble especificado por $H_0$ e $\beta$.

O último ponto que gostaríamos de ressaltar é quanto à estrutura analítica da Teoria Quântica de Campos à Temperatura Finita. Como sabemos, a introdução da velocidade do banho térmico possibilita uma nova dependência das amplitudes. No caso da auto-energia do campo de calibre, por exemplo, surge uma dependência explícita em $u \cdot p$ e $\sqrt{(u \cdot p)^2 - p^2}$ [7], o que no referencial de repouso do banho térmico, torna-se $p_0$ e $\vert\vec{p}\vert$. Isto não é nenhum problema, visto que este comportamento tem consequências físicas naturais. Como veremos no capítulo seguinte, certos limites em torno da origem do plano energia-momento estão associados com processos físicos bem específicos. O processo de blindagem de cargas dentro de um plasma, por exemplo, está associado com o limite estático, onde $p_0=0$ e $\vec{p} \rightarrow 0$. Existe também outro limite, conhecido como limite de onda longa, onde $\vec{p}=0$ e $p_0 \rightarrow 0$, relacionado com oscilações dentro de um plasma.