Como exemplo de uma teoria de campos não comutativa, vamos
considerar o modelo ![]() de um campo escalar real, expresso pela
seguinte ação
de um campo escalar real, expresso pela
seguinte ação![]() :
:
onde na segunda linha em ![]() estamos utilizando a
propriedade (4.10) do operador derivada.
estamos utilizando a
propriedade (4.10) do operador derivada.
Do cálculo acima podemos obter uma maneira muito simples de
introduzir a não comutatividade na TQC. Basta escrevermos a
lagrangiana do modelo usual com a troca dos produtos ordinários
entre funções pelos produtos-estrela. Mais ainda, também
consideramos que o produto-estrela entre duas funções dentro de uma
integração em ![]() não é afetado pela não
comutatividade do espaço, como vimos na
Eq. (4.14)
não é afetado pela não
comutatividade do espaço, como vimos na
Eq. (4.14)![]() . Desta forma, os
propagadores da teoria não são alterados pela não
comutatividade. Já os vértices passam a ser expressos, neste
exemplo, por:
. Desta forma, os
propagadores da teoria não são alterados pela não
comutatividade. Já os vértices passam a ser expressos, neste
exemplo, por:
onde definimos
![]() como:
como:
Na última passagem em (4.18) usamos o fato de ![]() estar sendo integrado em
estar sendo integrado em ![]() através da Eq. (4.17). Além
disso estamos definindo de forma compacta
através da Eq. (4.17). Além
disso estamos definindo de forma compacta
![]() e vamos considerar o
caso onde
e vamos considerar o
caso onde ![]()
![]()
Como um exemplo de cálculo, considere a correção de massa a um laço, neste caso dada por:
![$\displaystyle \int \frac{d^D k}{(2 \pi)^D} \frac{\frac{1}{3} \left[ 2
\cos^2(k\wedge p) + 1\right]}{k^2 + m^2}$](img639.png) |
|||
![$\displaystyle \int \frac{d^D k}{(2 \pi)^D} \frac{\frac{1}{3} \left[2 + \cos(2
k\wedge p) \right]}{k^2 + m^2}$](img640.png) |
|||
| (4.16) |
onde definimos:
| (4.17) |
e
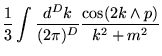 |
|||
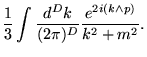 |
(4.18) |
Neste modelo simples, já podemos observar um aspecto interessante de
teorias não comutativas: a decomposição dos diagramas de
Feynman em duas componentes com comportamentos distintos, chamadas
planares e não planares. As contribuições planares (![]() no
nosso caso), a menos de uma fase que depende exclusivamente dos
momentos externos e fatores numéricos, são equivalentes às da
teoria comutativa. Já as não planares (
no
nosso caso), a menos de uma fase que depende exclusivamente dos
momentos externos e fatores numéricos, são equivalentes às da
teoria comutativa. Já as não planares (![]() ) misturam dentro
do integrando o momento externo com o de integração, por meio de
fatores oscilatórios. Partindo da Eq. (4.17) e da primeira
linha em (4.18), podemos generalizar esta discussão de
forma a obter a expressão dos vértices em uma teoria
qualquer. Assim, para uma interação contendo
) misturam dentro
do integrando o momento externo com o de integração, por meio de
fatores oscilatórios. Partindo da Eq. (4.17) e da primeira
linha em (4.18), podemos generalizar esta discussão de
forma a obter a expressão dos vértices em uma teoria
qualquer. Assim, para uma interação contendo ![]() campos
campos
![]() , temos que:
, temos que:
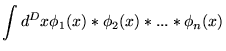 |
|||
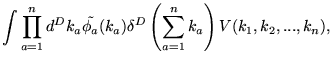 |
com
| (4.19) |
Como vemos, os vértices da teoria não comutativa
carregam uma fase que depende dos momentos e esta é a principal
diferença com relação ao caso comutativo. Mais ainda, é
possível demonstrar que ![]() sempre pode ser expresso em termos de
componentes planares e não planares, com as características
acima apresentadas [22,46].
sempre pode ser expresso em termos de
componentes planares e não planares, com as características
acima apresentadas [22,46].
Voltando ao cálculo que estamos desenvolvendo, em particular para
![]() , podemos perceber que
, podemos perceber que ![]() é quadraticamente
divergente. Já
é quadraticamente
divergente. Já ![]() não apresenta divergências no
ultravioleta, devido ao fator oscilatório no numerador. Este corte
das divergências ultravioletas, típico das contribuições
não planares, parece indicar que a expectativa inicial de melhora destas
divergências em uma teoria não comutativa se
justifica. Entretanto, como veremos a seguir, o que irá aparecer
agora é um outro tipo de divergência nestes diagramas na região
do infravermelho. Calculando
não apresenta divergências no
ultravioleta, devido ao fator oscilatório no numerador. Este corte
das divergências ultravioletas, típico das contribuições
não planares, parece indicar que a expectativa inicial de melhora destas
divergências em uma teoria não comutativa se
justifica. Entretanto, como veremos a seguir, o que irá aparecer
agora é um outro tipo de divergência nestes diagramas na região
do infravermelho. Calculando ![]() [47,22,44], chegamos a:
[47,22,44], chegamos a:
com
| (4.21) |
onde definimos
![]() . Além
disso, o parâmetro extra
. Além
disso, o parâmetro extra ![]() foi introduzido nas passagens
intermediárias de forma a facilitar as contas e deve tender a
infinito no resultado final. Se considerarmos este limite, obtemos:
foi introduzido nas passagens
intermediárias de forma a facilitar as contas e deve tender a
infinito no resultado final. Se considerarmos este limite, obtemos:
Por outro lado, se ao invés disso, mantivermos ![]() fixo e
fizermos
fixo e
fizermos ![]() na Eq. (4.24), temos
na Eq. (4.24), temos
Aqui aparece uma das principais características de teorias não
comutativas. Da Eq. (4.26) podemos perceber que embora
![]() seja finito para
seja finito para
![]() , ao contrário da
contribuição planar, ele apresenta uma divergência
infravermelha expressa pela singularidade em
, ao contrário da
contribuição planar, ele apresenta uma divergência
infravermelha expressa pela singularidade em ![]() : se
tentarmos retirar a não comutatividade, ou mesmo mantendo
: se
tentarmos retirar a não comutatividade, ou mesmo mantendo ![]() fixo, mas tendendo
fixo, mas tendendo
![]() a zero, recuperaremos a
divergência quadrática do caso comutativo. Por outro lado, a
inversão dos limites realizada em (4.27) é suficiente para
retirar a não comutatividade do modelo, mas recupera a divergência
quadrática, expressa em
a zero, recuperaremos a
divergência quadrática do caso comutativo. Por outro lado, a
inversão dos limites realizada em (4.27) é suficiente para
retirar a não comutatividade do modelo, mas recupera a divergência
quadrática, expressa em ![]() (de certa forma este parâmetro
está associado com o limite ultravioleta). Assim, as duas
divergências se misturam em uma teoria não comutativa e a
expectativa inicial de que a introdução de coordenadas que não
comutam poderia resolver o problema ultravioleta não se observa.
Este fenômeno é conhecido com mistura infravermelho-ultravioleta
(UV/IR) e é comum de teorias não comutativas [47]. Tal
comportamento pode ser melhorado em alguns modelos supersimétricos
[48].
(de certa forma este parâmetro
está associado com o limite ultravioleta). Assim, as duas
divergências se misturam em uma teoria não comutativa e a
expectativa inicial de que a introdução de coordenadas que não
comutam poderia resolver o problema ultravioleta não se observa.
Este fenômeno é conhecido com mistura infravermelho-ultravioleta
(UV/IR) e é comum de teorias não comutativas [47]. Tal
comportamento pode ser melhorado em alguns modelos supersimétricos
[48].
A quantização de teorias de calibre em espaços não
comutativos requer atenção na definição das derivadas
covariantes e transformações de calibre utilizadas, uma vez que
os produtos de campos agora dependem da ordem. Considere, por exemplo
a teoria de um campo escalar complexo ![]() acoplado a um campo de
calibre
acoplado a um campo de
calibre ![]() , expresso pela seguinte lagrangiana comutativa:
, expresso pela seguinte lagrangiana comutativa:
| (4.24) |
onde estamos considerando
![]() .
.
Como vimos anteriormente, a teoria não comutativa é obtida a
partir de
![]() através da troca do produto usual pelo
produto-estrela dos campos. Porém, se quisermos preservar a
invariância de calibre da teoria, devemos nos preocupar com a ordem
em que escrevemos tais produtos. Se fizermos o mapeamento:
através da troca do produto usual pelo
produto-estrela dos campos. Porém, se quisermos preservar a
invariância de calibre da teoria, devemos nos preocupar com a ordem
em que escrevemos tais produtos. Se fizermos o mapeamento:
devemos definir as transformações de calibre como sendo:
e a derivada covariante:
de forma a manter a invariância de calibre. Aqui
![]() representa a transformação de calibre
no espaço não comutativo e é expresso por:
representa a transformação de calibre
no espaço não comutativo e é expresso por:
| (4.27) |
A lagrangiana não comutativa assim obtida é escrita como;
| (4.28) |
e a teoria de campos descrita no espaço não comutativo
por ![]() é dita estar na representação fundamental à
esquerda.
é dita estar na representação fundamental à
esquerda.
Similarmente, podemos obter as representações à direita e adjunta. Por exemplo, na representação à direita, ao invés de considerarmos a versão não comutativa expressa pelas Eqs. (4.29) e (4.30), o mapeamento considerado é:
| (4.29) |
de tal forma que os campos escalares se transformam como:
| (4.30) |
A transformação do campo ![]() não se
altera e a derivada covariante passa a ser expressa por:
não se
altera e a derivada covariante passa a ser expressa por:
| (4.31) |
A teoria de Chern-Simons em ![]() dimensões é definida
incorporando à lagangiana do campo de calibre um termo do tipo:
dimensões é definida
incorporando à lagangiana do campo de calibre um termo do tipo:
Um comportamento interessante já pode ser percebido neste
modelo. Como no espaço não comutativo a ordem do produto dos
campos importa, agora, apesar de ainda estarmos considerando campos de
calibre abelianos, existe em ![]() um termo trilinear em
um termo trilinear em
![]() , típico de teorias não abelianas. Este
termo modifica intrinsicamente o comportamento dos modelos e como
veremos mais adiante, passaremos agora a obter vários comportamentos
qualitativamente mais próximos de uma teoria não abeliana.
, típico de teorias não abelianas. Este
termo modifica intrinsicamente o comportamento dos modelos e como
veremos mais adiante, passaremos agora a obter vários comportamentos
qualitativamente mais próximos de uma teoria não abeliana.