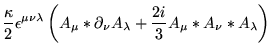 |
|||
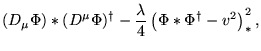 |
(4.33) |
Nesta seção iremos apresentar o cálculo da contribuição ao coeficiente de Chern-Simons proveniente do tensor de polarização a um laço. O modelo considerado é o Chern-Simons-Higgs, expresso em termos do produto-estrela como:
onde a derivada covariante considerada é
![]() . Na fase de simetria quebrada, de
maneira análoga ao que fizemos no capítulo anterior, para o
modelo de Maxwell-Chern-Simon-Higgs, vamos considerar
. Na fase de simetria quebrada, de
maneira análoga ao que fizemos no capítulo anterior, para o
modelo de Maxwell-Chern-Simon-Higgs, vamos considerar
![]() e decompor o campo escalar como
e decompor o campo escalar como
![]() , de tal forma que a lagrangiana
(4.37), em termos destes novos campos, torna-se:
, de tal forma que a lagrangiana
(4.37), em termos destes novos campos, torna-se:
onde estamos considerando o calibre
![]() , definido em (2.50), e definindo as seguintes massas:
, definido em (2.50), e definindo as seguintes massas:
| (4.35) |
Como vimos na seção anterior, os propagadores não são afetados pela não comutatividade e podem ser obtidos da maneira usual através dos termos bilineares dos campos. Desta forma, o propagador do campo de calibre no espaço euclidiano é dado por:
onde
![]() são as frequências de
Matsubara para o caso bosônico e estamos definindo uma nova massa
são as frequências de
Matsubara para o caso bosônico e estamos definindo uma nova massa
![]() para o campo de calibre como:
para o campo de calibre como:
Note que o propagador acima pode ser extraído da
Eq. (2.53), para o propagador do campo de calibre no modelo
Maxwell-Chern-Simons-Higgs, no limite
![]() , com
, com ![]() finito. Nesta situação, um dos pólos
de (2.53) deixa de existir e a teoria passa a ter uma
única massa física para o campo de calibre, expressa pela
Eq. (4.41). Já o propagador do campo escalar é o mesmo
utilizado no capítulo anterior, Eq. (3.30), ou seja:
finito. Nesta situação, um dos pólos
de (2.53) deixa de existir e a teoria passa a ter uma
única massa física para o campo de calibre, expressa pela
Eq. (4.41). Já o propagador do campo escalar é o mesmo
utilizado no capítulo anterior, Eq. (3.30), ou seja:
| (4.38) |
Com relação às contribuições em ![]() para os
vértices, além dos produtos usuais entre campos, novos termos
aparecem, exclusivos da teoria não comutativa. Um deles, o com
três campos de calibre, pode ser observado diretamente de
para os
vértices, além dos produtos usuais entre campos, novos termos
aparecem, exclusivos da teoria não comutativa. Um deles, o com
três campos de calibre, pode ser observado diretamente de ![]() , Eq. (4.36). Além deste, podemos notar a
presença de novos vértices que dependem de comutadores entre
campos e que no caso não comutativo não são nulos. No cálculo
que iremos desenvolver (isto é, a contribuição com quebra de paridade para
a função de dois pontos) somente dois diagramas contribuem (figura
(4.1)).
, Eq. (4.36). Além deste, podemos notar a
presença de novos vértices que dependem de comutadores entre
campos e que no caso não comutativo não são nulos. No cálculo
que iremos desenvolver (isto é, a contribuição com quebra de paridade para
a função de dois pontos) somente dois diagramas contribuem (figura
(4.1)).
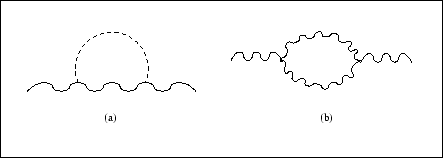 |
Considerando o primeiro diagrama, figura (4.1)(a), o termo que quebra paridade pode ser extraído diretamente (uma vez que só existe uma linha interna do campo de calibre) e é dado por:
![\begin{displaymath}
\Pi^{(a)}_{\mu\nu(PV)} \equiv {\cal{\pi}}^{(a)}_{\mu \nu}
(p...
...mbda} cos^2(k \wedge p)}{(k^2 +
M^2)[(p-k)^2 + m^2_{\sigma}]}.
\end{displaymath}](img697.png) |
(4.39) |
Para ![]() , a expressão acima torna-se:
, a expressão acima torna-se:
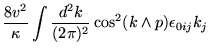 |
|||
![$\displaystyle \qquad \times \, T \sum_{n}\frac{1}{(k_0^2 +
w_M^2)\left[k_0^2 + (\vec{p} - \vec{k})^2 + m_{\sigma}^2(p)\right]}.$](img700.png) |
(4.40) |
Para calcular esta integral note que, enquanto o denominador contém
apenas somas em ![]() e
e ![]() e pode ser expandido em
pequenos momentos externos, usando uma expressão similar à
Eq. (3.46), o numerador contém o produto
e pode ser expandido em
pequenos momentos externos, usando uma expressão similar à
Eq. (3.46), o numerador contém o produto
![]() , que não necessariamente é pequeno para pequenos valores de
, que não necessariamente é pequeno para pequenos valores de
![]() . Para evitar possíveis problemas, vamos usar a
variável
. Para evitar possíveis problemas, vamos usar a
variável
![]() , tal que
, tal que
![]() . Desta forma, calculamos a soma em
. Desta forma, calculamos a soma em ![]() , expandindo
somente o denominador e deixamos a expansão em torno de
, expandindo
somente o denominador e deixamos a expansão em torno de
![]() para após o cálculo das integrais
espaciais. Seguindo estes passos, chegamos a:
para após o cálculo das integrais
espaciais. Seguindo estes passos, chegamos a:
onde usamos a Eq. (3.35) na soma em ![]() .
.
Utilizando a igualdade:
podemos reescrever a Eq. (4.45) como:
| (4.41) |
onde ![]() e
e ![]() são as contribuições planar
e não-planar a
são as contribuições planar
e não-planar a
![]() , respectivamente
dadas por:
, respectivamente
dadas por:
e
No cálculo da parte planar estão envolvidas as mesmas técnicas utilizadas no capítulo anterior. Assim, separando as partes independente e dependente da temperatura, chegamos a:
e
Vale ressaltar aqui que estamos apresentando também o
termo com temperatura nula porque ele assumirá um papel importante
na discussão da mistura das divergências IR/UV do modelo. Outro
ponto a ser destacado é que a Eq. (4.50) é exatamente
metade da Eq. (3.58), o que era de se esperar, uma vez que a
contribuição planar, a menos de uma fase, que é nula neste
caso, é igual ao cálculo direto do espaço comutativo (o fator
de meio aparece porque estamos considerando somente a parte planar;
como veremos a seguir, a outra metade virá do termo independente de
![]() em
em ![]() ). Calculando
). Calculando ![]() temos:
temos:
![$\displaystyle \frac{2 v^2}{\kappa} \int \frac{d^2k}{(2 \pi)^2}
\epsilon_{0ij} k...
...ft[1 - 2 \vec{k} \cdot \vec{p} \frac{\partial}{\partial
(m_{\sigma}^2)} \right]$](img722.png) |
|||
![$\displaystyle \qquad \times \, \left\{ \frac{1}{m_{\sigma}^2 - M^2}
\left[\frac...
...a w_M/2)}}{w_M} - \frac{\coth(\beta
w_{\sigma}/2)}{w_{\sigma}} \right] \right\}$](img723.png) |
|||
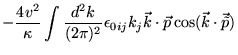 |
|||
![$\displaystyle \qquad \, \, \, \, \, \times \,
\frac{\partial}{\partial (m_{\sig...
... w_M/2)}}{w_M} -
\frac{\coth(\beta w_{\sigma}/2)}{w_{\sigma}} \right]
\right\}.$](img725.png) |
A integração em ![]() pode ser realizada com o uso de coordenadas
polares, figura (4.2), tais que:
pode ser realizada com o uso de coordenadas
polares, figura (4.2), tais que:
Desta forma, obtemos:
Agora usando que
![]() e
e
![]() , podemos simplificar a Eq. (4.53),
considerando somente os termos pares em
, podemos simplificar a Eq. (4.53),
considerando somente os termos pares em ![]() . Obtemos assim:
. Obtemos assim:
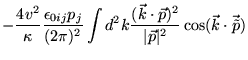 |
|||
![$\displaystyle \qquad \qquad \, \, \, \, \, \, \times
\frac{\partial}{\partial (...
...)}{w_M} - \frac{\coth(\frac{\beta
w_{\sigma}}{2})}{w_{\sigma}} \right] \right\}$](img733.png) |
|||
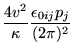 |
|||
![$\displaystyle \int_0^{\infty} k^3 d k \frac{\partial}{\partial
(m_{\sigma}^2)}\...
...)}}{w_M}
- \frac{\coth(\frac{\beta w_{\sigma}}{2})}{w_{\sigma}} \right]\right\}$](img735.png) |
|||
![$\displaystyle \qquad \times \int_0^{2
\pi} d \alpha \cos^2(\alpha) \cos\left[k p \theta \sin(\alpha)\right],$](img736.png) |
(4.45) |
onde
![]() .
.
O cálculo na variável angular, ![]() , pode ser efetuado de forma
exata em termos das funções de Bessel,
, pode ser efetuado de forma
exata em termos das funções de Bessel, ![]() [51]. Chegamos, assim, a:
[51]. Chegamos, assim, a:
onde utilizamos:
| (4.46) |
Integrais do tipo (4.55) em ![]() irão aparecer em todas as
amplitudes que iremos calcular. Assim, apresentaremos um cálculo
geral no apêndice (A). Aqui, nos restringiremos a listar os
resultados. Temos portanto:
irão aparecer em todas as
amplitudes que iremos calcular. Assim, apresentaremos um cálculo
geral no apêndice (A). Aqui, nos restringiremos a listar os
resultados. Temos portanto:
e
onde definimos uma nova variável ![]() como:
como:
Note, na Eq. (4.57), o surgimento de aparentes singularidades em
torno de ![]() (pólos de Seiberg). Como já dissemos
anteriormente, este tipo de divergência na região do
infravermelho, comum de teorias não comutativas [47],
expressa a mistura UV/IR. Neste caso, entretanto, ao expandirmos a
Eq. (4.57) em pequenos valores de
(pólos de Seiberg). Como já dissemos
anteriormente, este tipo de divergência na região do
infravermelho, comum de teorias não comutativas [47],
expressa a mistura UV/IR. Neste caso, entretanto, ao expandirmos a
Eq. (4.57) em pequenos valores de ![]() , apesar de
individualmente as divergências existirem, ocorre um cancelamento na
soma dos vários termos. Este resultado era esperado, uma vez que
já no caso comutativo a divergência ultravioleta não existe. Com
este particular comportamento, podemos escrever sem dificuldades o
limite
, apesar de
individualmente as divergências existirem, ocorre um cancelamento na
soma dos vários termos. Este resultado era esperado, uma vez que
já no caso comutativo a divergência ultravioleta não existe. Com
este particular comportamento, podemos escrever sem dificuldades o
limite ![]() , onde a não comutatividade é retirada da
teoria. Neste caso obtemos:
, onde a não comutatividade é retirada da
teoria. Neste caso obtemos:
e
onde no termo com ![]() estamos considerando também o
regime de altas temperaturas. Da Eqs. (4.60) e (4.61)
podemos obter o pedaço que faltava às Eqs. (4.49) e
(4.50) de forma a recuperar o limite comutativo.
estamos considerando também o
regime de altas temperaturas. Da Eqs. (4.60) e (4.61)
podemos obter o pedaço que faltava às Eqs. (4.49) e
(4.50) de forma a recuperar o limite comutativo.
O próximo passo é estudar a primeira correção às
Eqs. (4.60) e (4.61) com relação à
não comutatividade. No caso de temperatura nula, este estudo é
feito através de uma expansão em torno de ![]() . Chegamos
desta maneira a:
. Chegamos
desta maneira a:
| (4.50) |
Já para o termo dependente da temperatura, o parâmetro que surge
naturalmente é ![]() , e realizando uma expansão em torno de
, e realizando uma expansão em torno de
![]() , obtemos:
, obtemos:
Vamos agora estudar o segundo diagrama, figura (4.1)(b), expresso por:
Aqui temos uma estrutura de índices um pouco mais delicada e não podemos extrair diretamente o termo com quebra de paridade. Olhando somente para o numerador do integrando, temos:
![$\displaystyle \epsilon_{\mu \alpha \beta} \epsilon_{\sigma \rho
\nu} \left[ m^2...
...appa^2}{k^2 + \xi
m^2} - \kappa \epsilon_{\sigma\rho \delta} k_{\delta} \right]$](img764.png) |
(4.53) | ||
![$\displaystyle \left[ m^2 \delta_{\alpha \beta} - (k+ p)_{\alpha} (k + p)_{\beta...
...)^2 + \xi m^2} - \kappa \epsilon_{\alpha
\beta \gamma} (k+p)_{\gamma} \right] ,$](img765.png) |
e considerando somente os termos que contribuem para o cálculo envolvendo a quebra de paridade, chegamos a:
![$\displaystyle \kappa (m^2 - \xi \kappa^2) k \cdot (k+p)
\epsilon_{\mu \nu \alph...
...c{k_{\alpha}}{k^2 +\xi m^2} -
\frac{(k+p)_{\alpha}}{(k+p)^2 + \xi m^2} \right].$](img768.png) |
Incorporando este resultado à Eq. (4.64), podemos extrair o termo que quebra paridade como sendo:
![$\displaystyle 2 \kappa^2\int \frac{d^3
k}{(2 \pi)^3} \frac{\sin^2(k \wedge p) \epsilon_{\mu \nu \lambda}}{(m^4
+ \kappa^2 k^2) [m^4 + \kappa^2 (k+p)^2]}$](img771.png) |
|||
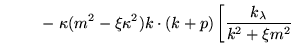 |
|||
![$\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad - \left. \left.
\frac{(k+p)_{\lambda}}{(k+p)^2 + \xi m^2} \right]\right\}.$](img774.png) |
O cálculo que segue não apresenta nenhuma novidade com relação ao anterior. Assim, sem discutir os detalhes, chegamos a:
e, no regime de altas temperaturas,
onde definimos a função ![]() como:
como:
| (4.56) |
Note que tanto (4.68) quanto (4.69) não apresentam um
termo independente de ![]() . Este resultado era esperado, uma vez
que este diagrama é uma contribuição puramente não
comutativa a
. Este resultado era esperado, uma vez
que este diagrama é uma contribuição puramente não
comutativa a ![]() , que deve desaparecer quando fizermos
, que deve desaparecer quando fizermos
![]() tender a zero (o termo trilinear em
tender a zero (o termo trilinear em ![]() na lagrangiana
desaparece neste limite). Matematicamente, podemos entender este
resultado diretamente da Eq. (4.64): para
na lagrangiana
desaparece neste limite). Matematicamente, podemos entender este
resultado diretamente da Eq. (4.64): para ![]() o seno
se anula e este diagrama desaparece. Outra questão
interessante que surge neste resultado é a dependência
explícita no parâmetro de calibre
o seno
se anula e este diagrama desaparece. Outra questão
interessante que surge neste resultado é a dependência
explícita no parâmetro de calibre ![]() . Note que este
comportamento veio do diagrama puramente não comutativo, fig
(4.1)(b). Aqui podemos reconhecer mais um aspecto que
assemelha este modelo ao caso não abeliano, uma vez que naquela situação
também obtemos uma dependência explícita do calibre neste
tipo de cálculo [49].
. Note que este
comportamento veio do diagrama puramente não comutativo, fig
(4.1)(b). Aqui podemos reconhecer mais um aspecto que
assemelha este modelo ao caso não abeliano, uma vez que naquela situação
também obtemos uma dependência explícita do calibre neste
tipo de cálculo [49].
Colecionando os resultados provenientes dos dois diagramas,
![]() a
a ![]() , obtemos:
, obtemos:
| (4.57) |
onde as componentes independente e dependente da temperatura são respectivamente dadas por:
e
Como já destacamos anteriormente, não existem singularidades no
infravermelho advindas das contribuições não planares, apesar
delas aparentemente estarem presentes nas expressões completas
(veja, por exemplo, Eq. (4.53)). Este resultado é esperado
porque o limite comutativo também não apresenta divergências
ultravioletas. Com relação ao termo com temperatura finita e
não nula, a contribuição em primeira ordem em ![]() apresenta uma dependência com a temperatura diferente da
contribuição comutativa, isto é, a contribuição planar
é proporcional a
apresenta uma dependência com a temperatura diferente da
contribuição comutativa, isto é, a contribuição planar
é proporcional a ![]() enquanto que a contribuição não planar
é proporcional a
enquanto que a contribuição não planar
é proporcional a ![]() . Esta diferença de comportamento
já foi encontrada em outros modelos [29] e pode
estar relacionada com a escolha de limites que estamos considerando,
isto é, a expansão em torno de pequenos valores de
. Esta diferença de comportamento
já foi encontrada em outros modelos [29] e pode
estar relacionada com a escolha de limites que estamos considerando,
isto é, a expansão em torno de pequenos valores de ![]() .
.