Tensor de Polarização no modelo Maxwell-Chern-Simons-Higgs

O modelo que iremos estudar inicialmente é o Maxwell-Chern-Simons-Higgs na fase quebrada, expresso pela seguinte lagrangiana:

$${\cal L} = - \frac{1}{4} F_{\mu \nu} F^{\mu \nu} + \frac{\ka... ...u} \Phi\vert^2 - \frac{\lambda}{4} (\vert\Phi\vert^2 - v^2)^2.$$ (3.26)

Expandindo o campo escalar em torno do seu valor esperado no vácuo, $\langle\vert\Phi\vert\rangle=v$, como $\Phi = v + \frac{1}{\sqrt{2}}(\sigma + i \chi)$ e considerando o calibre unitário, no qual o campo de Goldstone desacopla completamente do campo $A_{\mu }$, podemos reescrever ${\cal L}$ como:

$${\cal L} = - \frac{1}{4} F_{\mu \nu} F^{\mu \nu} + \frac{\kappa}{2} \epsilon... ... \nu \lambda} A_{\mu} \partial_{\nu} A_{\lambda} + \frac{m^2}{2} A_{\mu}A^{\mu}$$

$$+ \frac{1}{2} \partial_{\mu} \sigma \partial^{\mu} \sigma - \frac{m... ...u}A^{\mu} - \frac{\lambda v}{2 \sqrt{2}} \sigma^3 - \frac{\lambda}{16}\sigma^4.$$

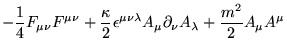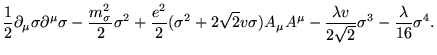Vamos efetuar o cálculo envolvendo temperatura no formalismo de tempo imaginário. Neste caso, os propagadores devem ser expressos no espaço euclidiano. Temos, portanto, para o campo de calibre:

$$D_{\mu \nu} (p) = \frac{1}{(p^2 + m_+^2)(p^2 + m_-^2)}$$

$$\times \left[\delta_{\mu \nu}(p^2 + m^2) + p_{\mu} p_{\nu} \frac{p^2 + m^2 + \kappa^2}{m^2} - \kappa \epsilon_{\mu \nu \lambda} p_{\lambda} \right],$$ (3.27)

e para o campo escalar $\sigma$:

$$D_{\sigma}^{(\beta)}(p)=\frac{1}{(p^2 + m_{\sigma}^2)},$$ (3.28)

onde $p = (w_n, \vec{p})$ e $w_n \equiv 2 \pi n T$ são as frequências de Matsubara para campos bosônicos. Também estamos utilizando as Eqs. (2.52) e (2.54), ou seja,

$$m^2= 2 e^2 v^2, \qquad m_{\sigma}^2= \lambda v^2,$$ (3.29)

e

$$m^2_{\pm} = \frac{\kappa^2 + 2 m^2 \pm \vert\kappa\vert\sqrt{\kappa^2 + 4 m^2}}{2}.$$ (3.30)

Novamente aqui vamos ressaltar a presença de dois pólos massivos para o campo de calibre, Eq. (3.29). Como já comentamos no capítulo anterior, este resultado é esperado, uma vez que estamos introduzindo na teoria dois diferentes mecanismos de geração de massa para este campo.

A seguir, iremos calcular o tensor de polarização a um laço.

Figura 3.2: Diagramas alça, fig. (a), e sol nascente, fig. (b), que contribuem para a auto-energia do fóton no modelo de Maxwell-Chern-Simons-Higgs e calibre unitário. As linhas pontilhadas representam o campo $\sigma$ e as onduladas, o $A_{\mu }$.

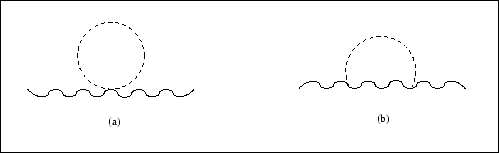Neste calibre, temos que calcular apenas dois diagramas: o alça e o sol nascente, figura (3.2). O diagrama alça contém apenas um termo que conserva paridade, ou seja,

$$\Pi_{\mu \nu}^{\mbox{al}} = \frac{1}{2} (2 e^2 \delta_{\mu \nu}) \frac{1}{\beta} \sum_n \int \frac{d^2k}{(2 \pi)^2} \frac{1}{k_0^2 + w_{\sigma}^2}$$

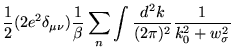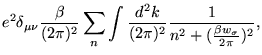$$= e^2 \delta_{\mu \nu} \frac{\beta}{(2\pi)^2} \sum_n \int \frac{d^2k}{(2 \pi)^2} \frac{1}{n^2 + (\frac{\beta w_{\sigma}}{2 \pi})^2},$$ (3.31)

onde $k_0 = 2 \pi n T$ e

$$w_{\sigma}^2=\vec{k}^2+ m_{\sigma}^2.$$ (3.32)

A soma em $n$ pode ser calculada de diversas maneiras. Nós iremos sempre utilizar a seguinte fórmula:

$$\sum_n f(n) = - \pi \mbox{Res} \left[ f(z) \cot{\pi z} \right],$$ (3.33)

onde os resíduos são calculados nos pólos de $f(z)$ [5,6]. Com o uso da expressão acima, $\Pi_{\mu \nu}^{\mbox{al}}$ torna-se:

$$\Pi_{\mu \nu}^{\mbox{al}} = \frac{1}{2} e^2 \delta_{\mu \nu}... ...pi)^2} \frac{1}{w_{\sigma}} \coth{\frac{\beta w_{\sigma}}{2}}.$$ (3.34)

Lembrando que:

$$\coth{\frac{\beta x}{2}}= 1 + \frac{2}{e^{\beta x}-1},$$ (3.35)

podemos extrair a parte dependente da temperatura como sendo:

$$\Pi_{\mu \nu}^{\mbox{al}}(T) = e^2 \delta_{\mu \nu} \int \fr... ...\nu} \frac{e^2}{2 \pi \beta} \ln{(1 - e^{-\beta m_{\sigma}})}.$$ (3.36)

Vale ressaltar que, apesar de termos conseguido obter um resultado exato, válido para qualquer temperatura, nem sempre isso é possível. De fato, como veremos a seguir, já no cálculo do diagrama sol nascente seremos forçados a considerar alguma aproximação para resolver as integrais espacias. Como iremos somar as contribuições provenientes dos dois diagramas no resultado final é interessante expressar $\Pi_{\mu \nu}^{\mbox{al}}(T)$ no regime que iremos estudar. Considerando, por exemplo, o limite de altas temperaturas, temos:

$$\Pi_{\mu \nu}^{\mbox{al}}(T) = - \delta_{\mu \nu} \frac{e^2}{2 \pi \beta} \ln(\beta m_{\sigma}).$$ (3.37)

O cálculo do diagrama sol nascente, figura (3.2)(b), é um pouco mais delicado por vários motivos. Primeiro, podemos observar que este diagrama apresenta dois termos, um com paridade conservada e outro com quebra de paridade, ou seja,

$$\Pi_{\mu \nu}^{\mbox{sn}} (p) = - 8 e^4 v^2 \frac{1}{\beta}\sum_n \int \frac{d^2k}{(2 \pi)^2} \fr... ...lambda} k_{\lambda}} { (k_0^2 + w_+^2)(k_0^2 + w_-^2)[(k+p)^2 + m_{\sigma}^2] }$$

$$\equiv \Pi_{\mu \nu (PC)}^{\mbox{sn}} (p) +\Pi_{\mu \nu (PV)}^{\mbox{sn}} (p),$$ (3.38)

onde definimos:

$$w^2 = \vec{k}^2 + m^2, \qquad w_{\pm}^2 = \vec{k}^2 + m_{\pm}^2.$$ (3.39)

Também introduzimos as componentes com paridade ímpar e par, respectivamente por:

$$\Pi_{\mu \nu (PV)}^{\mbox{sn}}(p) = 8 \kappa e^4 v^2 \epsilon_{\mu \nu \lambda} \frac{1}{\beta}$$

$$\times \sum_n \int \frac{d^2k}{(2 \pi)^2} \frac{k_{\lambda}}{[(k_0+p_0)^2 + (\vec{k}+\vec{p})^2 + m_{\sigma}^2](k_0^2 + w_+^2)(k_0^2 + w_-^2)},$$

e

$$\Pi_{\mu \nu (PC)}^{\mbox{sn}} (p) = - 8 e^4 v^2 \frac{1}{\beta}$$

$$\times \sum_n \int \frac{d^2k}{(2 \pi)^2} \frac{\delta_{\mu \nu}(k_0^2 +... ...2 + (\vec{k} + \vec{p})^2 + m_{\sigma}^2\right](k_0^2 + w_+^2)(k_0^2 + w_-^2)}.$$

Na análise que iremos desenvolver estaremos considerando dois casos: a. limite estático, onde $p_0=0$ e $\vec{p} \rightarrow 0$, e b. limite de onda longa, onde $\vec{p}=0$ e $p_0 \rightarrow 0$. A escolha destes limites está diretamente relacionada com a obtenção das massas físicas do sistema. As massas elétrica e magnética, por exemplo, podem ser obtidas, como já apresentamos na introdução deste capítulo, do limite estático do tensor de polarização, Eq. (3.21).