Partindo da Eq. (3.42) e considerando ![]() , temos:
, temos:
Olhando em separado para cada uma das contribuições a
![]() (
(![]() e
e ![]() ), é imediato concluir que:
), é imediato concluir que:
| (3.40) |
devido à antisimetria do integrando na Eq. (3.44) (a
soma em ![]() para
para ![]() é ímpar). Consequentemente, nos
resta calcular apenas a componente
é ímpar). Consequentemente, nos
resta calcular apenas a componente
![]() . Podemos ainda, antes de efetuar a soma,
expandir o integrando em torno de
. Podemos ainda, antes de efetuar a soma,
expandir o integrando em torno de ![]() . Utilizando:
. Utilizando:
obtemos, para pequenos momentos,
![$\displaystyle 8 \kappa e^4 v^2 \epsilon_{0ij}
\frac{1}{\beta} \int \frac{d^2k}{...
...eft[1 + 2 \vec{p}
\cdot \vec{k} \frac{\partial}{\partial (m_{\sigma}^2)}\right]$](img335.png) |
|||
| (3.41) |
O primeiro termo no integrando (linear em ![]() ) se anula devido a
antisimetria. Chegamos assim a:
) se anula devido a
antisimetria. Chegamos assim a:
O próximo passo consiste em efetuar a soma em
![]() . Com
o uso da Eq. (3.35), chegamos a:
. Com
o uso da Eq. (3.35), chegamos a:
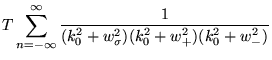 |
|||
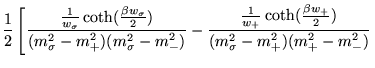 |
|||
![$\displaystyle \, \, \, \, \, + \left.\frac {\frac{1}{w_-} \coth(\frac{\beta
w_-}{2}) } { (m_{\sigma}^2 - m_-^2 ) (m_+^2 - m_-^2 ) }\right].$](img345.png) |
(3.43) |
Substituindo este resultado em
![]() , Eq. (3.48), temos:
, Eq. (3.48), temos:
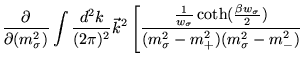 |
|||
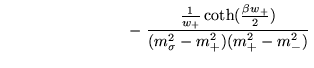 |
|||
![$\displaystyle \qquad \qquad \qquad \qquad + \left.\frac {
\frac{1}{w_-} \coth(\frac{\beta
w_-}{2}) } { (m_{\sigma}^2 - m_-^2 ) (m_+^2 - m_-^2 )
}\right].$](img349.png) |
A parte com ![]() da expressão acima pode ser extraída
diretamente com o uso da Eq. (3.37) e concorda com resultados
obtidos no formalismo usual [40] (vale salientar que esta
comparação deve levar em conta o fato de estarmos fazendo o
cálculo no espaço euclidiano). A correção dependente da
temperatura é dada por:
da expressão acima pode ser extraída
diretamente com o uso da Eq. (3.37) e concorda com resultados
obtidos no formalismo usual [40] (vale salientar que esta
comparação deve levar em conta o fato de estarmos fazendo o
cálculo no espaço euclidiano). A correção dependente da
temperatura é dada por:
onde estamos utilizando a função distribuição bosônica, ou seja,
| (3.44) |
As integrais que aparecem na Eq. (3.51) podem ser expressas em
termos da função ![]() , definida como [5]:
, definida como [5]:
e, em geral, não podem ser calculadas de maneira
exata. É possível, porém, obter os seus limites para pequenos
valores de ![]() [5,39]. No apêndice (A) iremos calcular
explicitamente
[5,39]. No apêndice (A) iremos calcular
explicitamente ![]() . Com o uso deste resultado,
podemos obter a integral que aparece na Eq. (3.51), ou seja,
. Com o uso deste resultado,
podemos obter a integral que aparece na Eq. (3.51), ou seja,
onde ![]() é a função Zeta de Riemann
[51]. Com o uso de (3.54), extraímos o
termo dominante, a altas temperaturas, de
é a função Zeta de Riemann
[51]. Com o uso de (3.54), extraímos o
termo dominante, a altas temperaturas, de
![]() , Eq. (3.51), como sendo [25]:
, Eq. (3.51), como sendo [25]:
onde definimos:
| (3.48) |
e
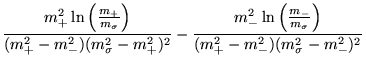 |
|||
| (3.49) |
Deste resultado pode-se também obter o limite de uma
teoria de Chern-Simons pura, no qual o termo de Maxwell é retirado
da lagrangiana. Este limite é obtido de (3.55)
considerando-se
![]() , com
, com ![]() finito. Neste caso,
finito. Neste caso,
![]() ,
,
![]() e (3.55) torna-se:
e (3.55) torna-se:
No próximo capítulo iremos obter o mesmo resultado de uma outra maneira.
O termo com paridade conservada pode ser calculado explicitamente, utilizando passos muito semelhantes aos acima apresentados. Existe, porém, um caminho alternativo para este cálculo, se lembrarmos que, à temperatura finita, a auto-energia do campo de calibre pode ser parametrizada, na fase de simetria quebrada, como [15,7,26]:
onde
| (3.52) |
com
| (3.53) |
e ![]() sendo a velocidade do banho térmico (no
referencial de repouso expressa por
sendo a velocidade do banho térmico (no
referencial de repouso expressa por
![]() ). Os
dois primeiros termos são os usuais, associados com a
decomposição do tensor de polarização a
). Os
dois primeiros termos são os usuais, associados com a
decomposição do tensor de polarização a ![]() . Já
. Já
![]() aparece porque estamos considerando o sistema na fase
quebrada. Usando esta decomposição podemos, através de uma
álgebra direta, obter cada uma das componentes associadas com o
termo de paridade conservada. Assim, temos:
aparece porque estamos considerando o sistema na fase
quebrada. Usando esta decomposição podemos, através de uma
álgebra direta, obter cada uma das componentes associadas com o
termo de paridade conservada. Assim, temos:
e
No limite estático , as componentes acima tornam-se:
e
| (3.55) |
Ao invés de calcularmos diretamente
![]() , é muito mais simples calcular
, é muito mais simples calcular ![]() ,
, ![]() e
e ![]() que
dependem somente de
que
dependem somente de ![]() ,
, ![]() e
e
![]() . Além disso, estas
componentes são suficientes para determinarmos as massas elétrica
e magnética do sistema.
. Além disso, estas
componentes são suficientes para determinarmos as massas elétrica
e magnética do sistema.
A componente ![]() da Eq. (3.43) é dada, para
da Eq. (3.43) é dada, para ![]() , por:
, por:
![\begin{displaymath}
\Pi_{00}^{\mbox{sn}}(\vec{p}) = - 4 e^2 m^2 \frac{1}{\beta} ...
...c{p})^2 + m_{\sigma}^2 ]
(k_0^2 + w_+^2 ) (k_0^2 + w_-^2 ) }.
\end{displaymath}](img389.png) |
(3.56) |
Novamente aqui, utilizamos passos similares aos utilizados
no cálculo do termo com quebra de paridade: a expansão em pequenos
momentos (neste caso estamos interessados no termo independente de
![]() ) e a soma em
) e a soma em ![]() . Considerando somente a
contribuição dependente da temperatura, no limite de altas
temperaturas chegamos a [26]:
. Considerando somente a
contribuição dependente da temperatura, no limite de altas
temperaturas chegamos a [26]:
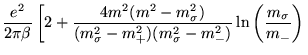 |
|||
![$\displaystyle \qquad - \left. \frac{4
m^2 (m^2 - m_+^2)}{(m_{\sigma}^2 - m_+^2)(m_+^2 -
m_-^2)}\ln\left(\frac{m_+}{m_-}\right) \right],$](img393.png) |
(3.57) |
onde nós empregamos, de maneira análoga ao cálculo da Eq. (3.54),
| (3.58) |
e
| (3.59) |
O cálculo de ![]() é semelhante ao de
é semelhante ao de ![]() e
fornece, a altas temperaturas, o resultado [26]:
e
fornece, a altas temperaturas, o resultado [26]:
 |
|||
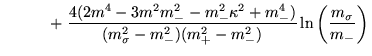 |
|||
![$\displaystyle \qquad \, \, \, \, \, \, - \left. \frac{4(2 m^4 -
3 m^2 m_+^2 - m...
...sigma}^2 - m_+^2)(m_+^2 -
m_-^2)}\ln\left(\frac{m_{\sigma}}{m_+}\right)\right].$](img400.png) |
Finalmente,
| (3.60) |
Segue, portanto que, no limite estático,
e
| (3.61) |
Adicionando a este resultado a contribuição proveniente do diagrama alça, chegamos finalmente a
e