Introdução

Nesta seção vamos descrever alguns dos principais aspectos envolvendo a teoria quântica de campos não comutativa, necessários ao entendimento das seções seguintes. Não será nosso objetivo demonstrar as propriedades, uma vez que boas revisões deste tópico podem ser encontradas na literatura [22].

Na TQC usual trabalhamos com funções $f(x)$ definidas no espaço $R^D$ ``comutativo'', ou seja, onde as variáveis $x^{\mu}$ satisfazem:

$$[x^{\mu},x^{\nu}]=0.$$ (4.1)

Introduzimos a não comutatividade definindo um novo espaço $R^D_{\theta}$, onde as variáveis $x^{\mu}$ passam a ser mapeadas em operadores $\hat{x}^{\mu}$, satisfazendo à seguinte relação de comutação:

$$[\hat{x}^{\mu},\hat{x}^{\nu}]= i \theta^{\mu \nu}.$$ (4.2)

Aqui, $\theta^{\mu \nu}$ é uma matriz antisimétrica, que estamos considerando constante. Para ver como produtos entre funções são abordados neste novo espaço, vamos considerar o seguinte. Inicialmente, definimos um elemento em $R^D_{\theta}$ como:

$$\hat{W}[f] \equiv \int \frac{d^D k}{(2 \pi)^D} \tilde{f}(k) \hat{T}(k),$$ (4.3)

onde $\tilde{f}(k)$ é a transformada de Fourier de $f(x)$ e $\hat{T}(k)$ é dado por:

$$\hat{T}(k) \equiv e^{- i k \cdot \hat{x}}.$$ (4.4)

Como podemos perceber da definição (4.3), para cada $f(x)$ com $x$ pertencente a $R^D$ existe um $\hat{W}[f]$ em $R_{\theta}^D$. Mais explicitamente, através de um operador $\hat{\Delta}(x, \hat{x})$, expresso por:

$$\hat{\Delta}(x, \hat{x}) \equiv \int \frac{d^D k}{(2 \pi)^D} e^{i k \cdot \hat{x}} e^{- i k \cdot x },$$ (4.5)

podemos relacionar $\hat{W}[f]$ diretamente com $f(x)$, ou seja,

$$\hat{W}[f] = \int d^D x f(x) \hat{\Delta}(x, \hat{x}).$$ (4.6)

Além disso, podemos inverter $\hat{W}[f]$ com o uso de $\hat{\Delta}(x, \hat{x})$ de forma a obter $f(x)$ em termos de $\hat{W}[f]$ como sendo:

$$f(x) = \mbox{Tr} \left[ \hat{W}[f] \hat{\Delta}(x, \hat{x}) \right].$$ (4.7)

Na expressão acima, a operação de traço é realizada em $R_{\theta}^D$ e é definida por:

$$\mbox{Tr} \, \hat{W}[f] \equiv \int d^D x f(x),$$ (4.8)

com a normalização $\mbox{Tr} \, \hat{\Delta}(x, \hat{x}) \equiv 1$.

A operação de derivação é expressa em $R_{\theta}^D$ através de um operador $\hat{\partial}_{\mu}$ definido a partir das seguintes relações de comutação:

$$[\hat{\partial}_{\mu},\hat{x}^{\nu}]= \delta_{\mu}^{\nu}, \qquad [\hat{\partial}_{\mu},\hat{\partial}_{\nu} ] = 0.$$ (4.9)

Uma característica importante de $\hat{\partial}_{\mu}$, que será utilizada na versão não comutativa da teoria quântica de campos, é que o comutador dele com $\hat{W}[f]$ atua como uma derivada ordinária em $f(x)$, ou seja,

$$[ \hat{\partial}_{\mu}, \hat{W}[f]] = \hat{W}[\partial_{\mu} f].$$ (4.10)

A próxima propriedade que estamos interessados em discutir é a multiplicação entre dois elementos $\hat{W}[f]$ e $\hat{W}[g]$. Como veremos a seguir, desta relação iremos naturalmente definir o produto Grönewold-Moyal entre duas funções $f(x)$ e $g(x)$ (também conhecido como produto-estrela): com o uso das Eqs. (4.6) e (4.7), pudemos relacionar $\hat{W}[f]$ e $f(x)$ de maneira única através de $\hat{\Delta}(x, \hat{x})$; de maneira análoga, com o uso do produto-estrela iremos relacionar a multiplicação entre $\hat{W}[f]$ e $\hat{W}[g]$ com as respectivas funções $f(x)$ e $g(x)$. Esta relação é dada por:

$$\hat{W}[f] \hat{W}[g] = \hat{W} [f \ast g],$$ (4.11)

onde está sendo definido o produto-estrela entre $f(x)$ e $g(x)$, $(f \ast g)(x)$, como sendo:

$$f (x) \ast g (x) \equiv \int \int \frac{d^D k}{(2 \pi)^D} \frac{d^D k'}{(2 \pi)^D} \tilde... ...^{- \frac{i}{2} \theta^{\mu \nu} k_{\mu} k'_{\nu}} e^{k'_{\lambda} x^{\lambda}}$$

$$= \lim_{x \rightarrow y} f(x) \left(e^{\frac{i}{2} \partial_{x_{\mu}} \theta^{\mu \nu} \partial_{y_{\nu}}}\right) g(y)$$

$$= f(x) g(x)$$

$$+ \sum_{n=1}^{\infty} \left(\frac{i}{2}\right)^n \frac{1}{n!} \thet... ...l_{\mu_1} ... \partial_{\mu_n} f(x) \partial_{\nu_1} ... \partial_{\nu_n} g(x).$$

Finalmente, como consequência da definição do traço, Eq. (4.8), e do produto-estrela, Eq. (4.11), temos que:

$$\mbox{Tr} \hat{W}[f_1] \hat{W}[f_2] ... \hat{W}[f_n] = \int d^D x f_1(x) \ast f_2(x) \ast ... \ast f_n(x),$$ (4.12)

e portanto, pelas propriedades do traço no lado esquerdo da expressão acima, podemos perceber que o produto-estrela de um número qualquer de funções é cíclico dentro de uma integral em $x$. Em particular, para duas funções $f_1(x)$ e $f_2(x)$, vale que:

$$\mbox{Tr} \hat{W}[f_1] \hat{W}[f_2] = \int d^D x f_1(x) \ast f_2(x) = \int d^D x f_1(x) f_2(x),$$ (4.13)

ou seja, a integração em $x$ do produto-estrela de duas funções quaisquer, é idêntica à integração do produto usual. Esta propriedade vai ser muito importante na definição da teoria quântica e mostra que os propagadores, e de forma mais geral, a teoria livre, não são alterados pela introdução de coordenadas que não comutam.

Em resumo, criamos uma correspondência entre funções em $R^D$ e elementos em $R^D_{\theta}$ através de:

$$R^D \leftrightarrow R^D_{\theta},$$

$$f(x) \leftrightarrow \hat{W}[f],$$

$$f(x) g(x) \leftrightarrow \hat{W}[f] \hat{W}[g] \equiv \hat{W}[f \ast g],$$

$$\int d^D x f(x) \leftrightarrow \mbox{Tr} \, \hat{W}[f],$$

$$\int d^D x f_1(x) ... f_n(x) \leftrightarrow \mbox{Tr} \hat{W}_1[f]... \hat{W}_n[f]$$

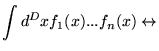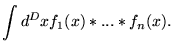$$\equiv \int d^D x f_1(x) \ast ... \ast f_n(x).$$ (4.14)