When Fourier series are employed to solve partial differential
equations, low-pass filters can be used to regularize divergent series
that may appear. In this paper we show that the linear low-pass filters
defined in a previous paper can be interpreted in terms of the
correspondence between Fourier Conjugate (FC) pairs of Definite Parity
(DP) Fourier series and inner analytic functions, which was established
in earlier papers. The action of the first-order linear low-pass filter
corresponds to an operation in the complex plane that we refer to as
``singularity splitting'', in which any given singularity of an inner
analytic function on the unit circle is replaced by two softer
singularities on that same circle, thus leading to corresponding DP
Fourier series with better convergence characteristics. Higher-order
linear low-pass filters can be easily defined within the unit disk of
the complex plane, in terms of the first-order one. The construction of
infinite-order filters, which always result in
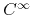
real
functions over the unit circle, and in corresponding DP Fourier series
which are absolutely and uniformly convergent to these functions, is
presented and discussed.