The Low-Pass Filter on the Complex Plane

According to the correspondence established in [1], to each FC pair of DP Fourier series corresponds an inner analytic function $w(z)$ within the open unit disk. Each operation performed on the DP Fourier series corresponds to a related operation on the inner analytic function, possibly represented by its Taylor series around the origin. For example, differentiation of the DP Fourier series with respect to their real variable $\theta$ corresponds to logarithmic differentiation of $w(z)$ with respect to $z$, as shown in [2]. If we imagine that the first-order low-pass filter is to be implemented on the DP real functions $f_{\rm c}(\theta)$ and $f_{\rm s}(\theta)$ associated to the DP Fourier series, where for $z=\rho\exp(\mbox{\boldmath$\imath$}\theta)$ and $\rho=1$ we have

$$w(z) = f_{\rm c}(\theta)+\mbox{\boldmath$\imath$}f_{\rm s}(\theta),$$

then it is clear that a corresponding filtering operation over $w(z)$ must exist within the open unit disk. In this section we will give the definition of this filtering operation on the complex plane, and derive some of its properties.

Consider then an inner analytic function $w(z)$, with $z=\rho\exp(\mbox{\boldmath$\imath$}\theta)$ and $0\leq\rho\leq 1$. We define from it the corresponding filtered complex function, using the real angular range parameter $0<\epsilon\leq\pi$, by

$$w_{\epsilon}(z) = -\, \frac{\mbox{\boldmath$\imath$}}{2\... ...minus}}^{z_{\oplus}}dz'\, \frac{1}{z'}\, w\!\left(z'\right),$$ (3)

involving an integral over the arc of circle illustrated in Figure 1, where the two extremes are given by

$$\begin{eqnarray*} z_{\ominus} & = & z\,{\rm e}^{-\mbox{\boldmath$\imath$}\eps... ... = & \rho\,{\rm e}^{\mbox{\boldmath$\imath$}(\theta+\epsilon)}. \end{eqnarray*}$$

Figure 1: Illustration of the definition of the first-order linear low-pass filter within the unit disk of the complex plane. The average is taken over the arc of circle from $z_{\ominus }$ to $z_{\oplus }$.

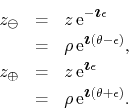
It is important to observe that this definition can be implemented at all the points of the unit disk, with the single additional proviso that at $z=0$ the filter be defined as the identity. Note that the definition in Equation (3) has the form of a logarithmic integral, which is the inverse operation to the logarithmic derivative, as defined and discussed in [2]. What we are doing here is to map the value of the function $w(z)$ at $z$ to the average of $w(z)$ over the symmetric arc of circle of angular length $2\epsilon$ around $z$, with constant $\rho$. This defines a new complex function $w_{\epsilon }(z)$ at that point. Since on the arc of circle we have that $z'=\rho\exp(\mbox{\boldmath$\imath$}\theta')$ and hence that $dz'=\mbox{\boldmath$\imath$}z'd\theta'$, we may also write the definition as

$$w_{\epsilon}(z) = \frac{1}{2\epsilon} \int_{\theta-\epsilon}^{\theta+\epsilon}d\theta'\, w\!\left(\rho,\theta'\right),$$

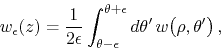
which makes the averaging process explicitly clear. As one might expect, just as the logarithmic differentiation of inner analytic functions corresponds to derivatives with respect to $\theta$, the logarithmic integration corresponds to integrals on $\theta$. Note that for $\epsilon=\pi$ the complex filtered function $w_{\epsilon }(z)$ is simply a constant function, possibly with removable singularities on the unit circle. Since our real functions here, being the real or imaginary parts of inner analytic functions, are zero-average functions, that constant is actually zero, for all inner analytic functions.

Let us show that $w_{\epsilon }(z)$ is an inner analytic function, as defined in [1]. Note that since $w(z)$ is an inner analytic function, it has the property that $w(0)=0$. Therefore we see that because $w(0)=0$ the integrand in Equation (3) is analytic within the open unit circle, if defined by continuity at $z=0$. Consider therefore the integral over the closed oriented circuit shown in Figure 1,

$$\int_{0}^{z_{\ominus}}dz'\, \frac{1}{z'}\, w\!\left(z'\ri... ..._{\oplus}}^{0}dz'\, \frac{1}{z'}\, w\!\left(z'\right) = 0.$$ (4)

Since the contour is closed and the integrand is analytic on it and within it, this integral is zero due to the Cauchy-Goursat theorem. It follows that we have

$$\int_{z_{\ominus}}^{z_{\oplus}}dz'\, \frac{1}{z'}\, w\!\l... ...nt_{0}^{z_{\ominus}}dz'\, \frac{1}{z'}\, w\!\left(z'\right).$$

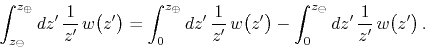
These last two integrals give the logarithmic primitive of $w(z)$ at the two ends of the arc, as defined in [2]. According to that definition the logarithmic primitive of $w(z)$ is given by

$$w^{-1\!\mbox{\Large$\cdot$}\!}(z) = \int_{0}^{z}dz'\, \frac{1}{z'}\, w\!\left(z'\right),$$

where we are using the notation for the logarithmic primitive introduced in that paper. The logarithmic primitive $w^{-1\!\mbox{\Large$\cdot$}\!}(z)$ is an inner analytic function within the open unit disk, as shown in [2]. It follows that we have

$$\int_{z_{\ominus}}^{z_{\oplus}}dz'\, \frac{1}{z'}\, w\!\l... ...}(z_{\oplus}) - w^{-1\!\mbox{\Large$\cdot$}\!}(z_{\ominus}).$$

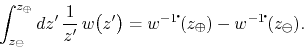
Since the logarithmic primitive $w^{-1\!\mbox{\Large$\cdot$}\!}(z)$ is an inner analytic function, and since the functions $z_{\ominus}(z)$ and $z_{\oplus}(z)$ are also rotated inner analytic functions, as can easily be verified, it is reasonable to think that the right-hand side of this equation is an inner analytic function. We have therefore for the filtered complex function

$$w_{\epsilon}(z) = -\, \frac{\mbox{\boldmath$\imath$}}{2\... ...us}) - w^{-1\!\mbox{\Large$\cdot$}\!}(z_{\ominus}) \right],$$ (5)

which indicates that $w_{\epsilon }(z)$ is an inner analytic function as well. In fact, the analyticity of $w_{\epsilon }(z)$ is evident, since it is a linear combination of two analytic functions within the open unit disk. We must also show that $w_{\epsilon}(0)=0$ and that $w_{\epsilon }(z)$ reduces to a real function on the interval $(-1,1)$ of the real axis, which are the additional properties defining an inner analytic function, as given in [1]. It is easy to check directly that $w_{\epsilon}(0)=0$, since $w^{-1\!\mbox{\Large$\cdot$}\!}(0)=0$, given that the logarithmic primitive is an inner analytic function. In order to establish the remaining property, we replace $z$ by a real $x$ in the filtered function, and taking the complex conjugate of that function with argument $x$ we get

$$w_{\epsilon}^{*}(x) = \frac{\mbox{\boldmath$\imath$}}{2\e... ...rm e}^{-\mbox{\boldmath$\imath$}\epsilon}\right) \right]^{*}.$$

Now, since $w^{-1\!\mbox{\Large$\cdot$}\!}(z)$ is an inner analytic function, it follows that $w^{-1\!\mbox{\Large$\cdot$}\!}(x)$ is a real function. Therefore the only relevant participation of the number $\mbox{\boldmath$\imath$}$ in the quantity within the brackets in the expression above is that introduced explicitly via the arguments. We have therefore, taking the complex conjugates on the right-hand side,

$$\begin{eqnarray*} w_{\epsilon}^{*}(x) & = & \frac{\mbox{\boldmath$\imath$}}{2... ...$\imath$}\epsilon}\right) \right] \\ & = & w_{\epsilon}(x), \end{eqnarray*}$$

so that $w_{\epsilon }(z)$ reduces to a real function on the interval $(-1,1)$ of the real axis. This establishes, therefore, that the filtered complex function $w_{\epsilon }(z)$ is in fact an inner analytic function. In addition to this, since logarithmic integration softens the singularities of $w(z)$ by one degree, as discussed in [2], we see that $w_{\epsilon }(z)$ will have all its singularities softened by one degree as compared to those of $w(z)$.

Observe that, if we take the limit $\rho\to 1$ to the unit circle in such a way that $z$ tends to a singularity of $w(z)$ at the position $\theta$, it immediately follows that $w_{\epsilon }(z)$ has two singularities, each softened by one degree, at the positions $(\theta-\epsilon)$ and $(\theta+\epsilon)$. What we have here is what we will refer to as the process of singularity splitting, for we see that the application of the filter has the effect of interchanging a harder singularity at $\theta$ by two softer singularities at $(\theta-\epsilon)$ and $(\theta+\epsilon)$. In particular, this will always decrease the degree of hardness, or increase the degree of softness, of all the dominant singularities on the unit circle, by one degree. This in turn is important because the dominant singularities determine the level and mode of convergence of the DP Fourier series, as discussed in [2].

Observe that the filtering operation does not stay within a single integral-differential chain of inner analytic functions, as defined in [2], since it changes the location of the singularities of the inner analytic function it is applied to. Instead, it passes to another such chain, while at the same time changing to the next link in the new chain, in the softening direction, since it softens the singularities by one degree. The new function reached in this way is not directly related to the original one by straight logarithmic integration. The new function is, however, close to the original function, so long as $\epsilon$ is small, according to a criterion that has a clear physical meaning, as explained in [3].

Since the complex-plane definition of the first-order low-pass filter in the open unit disk reproduces the definition of the filter as given in Equation (1) directly in terms of the corresponding real functions on the unit circle, it also reproduces all the properties of the filter when acting on the real functions, which were discussed and demonstrated in [3]. In some cases there are corresponding properties of the filter in terms of the complex functions. By construction it is clear that, just as $w(z)$, the function $w_{\epsilon }(z)$ is periodic in $\theta$, with period $2\pi$, which is a generalization to the complex plane of one of the properties of the filter [9]. In addition to this, since it acts on inner analytic functions, which are analytic and thus always continuous and differentiable, it is quite clear that the filter becomes the identity operation in the $\epsilon\to 0$ limit. We can see this from the complex-plane definition in Equation (5). If we consider the variation of $\theta$ between $z_{\oplus }$ and $z_{\ominus }$, which is given in terms of the parameter $\epsilon$ by $\delta\theta=2\epsilon$, and we take the $\epsilon\to 0$ limit of that expression, we get

$$\begin{eqnarray*} \lim_{\epsilon\to 0} w_{\epsilon}(z) & = & -\mbox{\boldmat... ...\oplus})-w^{-1\!\mbox{\Large$\cdot$}\!}(z_{\ominus})}{\delta z}, \end{eqnarray*}$$

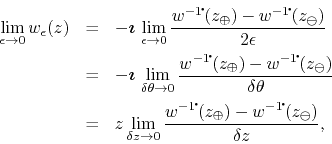
where we used the fact that in the limit $\delta z=\mbox{\boldmath$\imath$}z\delta\theta$. The limit above defines the logarithmic derivative, so that we have

$$\begin{eqnarray*} \lim_{\epsilon\to 0} w_{\epsilon}(z) & = & z\, \frac{d}{dz}w^{-1\!\mbox{\Large$\cdot$}\!}(z) \\ & = & w(z), \end{eqnarray*}$$

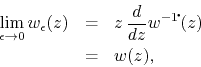
since we have the logarithmic derivative of the logarithmic primitive, and the operations of logarithmic differentiation and logarithmic integration are the inverses of one another. This establishes that in the $\epsilon\to 0$ limit the filter becomes the identity when acting on the inner analytic functions, which is a generalization to the complex plane of another property of the filter [7]. In fact, this property within the open unit disk is somewhat stronger than the corresponding property on the unit circle, since in this case we have exactly the identity in all cases, while in the real case we had only the identity almost everywhere.

Taken in the light of the classification of singularities and modes of convergence which was given in [2], we can see immediately the consequences of this process of singularity splitting on the mode of convergence of the DP Fourier series associated to the inner analytic function, and on the analytic character of the corresponding DP real functions. Let us recall from the earlier papers [1] and [2] that given an inner analytic function

$$w(z) = f_{\rm c}(\rho,\theta)+\mbox{\boldmath$\imath$}f_{\rm s}(\rho,\theta),$$

where $z=\rho\exp(\mbox{\boldmath$\imath$}\theta)$, and its Taylor series around $z=0$,

$$w(z) = \sum_{k=1}^{\infty} a_{k}z^{k},$$

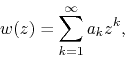
which is convergent at least on the open unit disk, it follows that on the unit circle we have the real functions $f_{\rm c}(\theta)=f_{\rm c}(1,\theta)$ and $f_{\rm s}(\theta)=f_{\rm s}(1,\theta)$, associated to the FC pair of DP Fourier series

$$\begin{eqnarray*} f_{\rm c}(\theta) & = & \sum_{k=1}^{\infty} a_{k}\cos(k\th... ...{\rm s}(\theta) & = & \sum_{k=1}^{\infty} a_{k}\sin(k\theta). \end{eqnarray*}$$

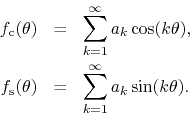
After the action of the filter we have corresponding relations for the filtered functions,

$$\begin{eqnarray*} w_{\epsilon}(z) & = & f_{\epsilon,{\rm c}}(\rho,\theta)+\mb... ...theta) & = & \sum_{k=1}^{\infty} a_{\epsilon,k}\sin(k\theta). \end{eqnarray*}$$

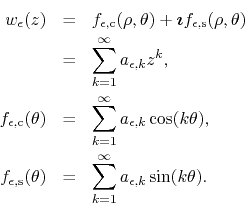
The results obtained in [2] relate the nature of the dominant singularities of $w(z)$ on the unit circle with the mode of convergence of the corresponding DP Fourier series and with the analytical character of the corresponding DP real functions $f_{\rm c}(\theta)$ and $f_{\rm s}(\theta)$, for a large class of inner analytic functions and corresponding DP real functions. The same relations also hold for $w_{\epsilon }(z)$, of course. Assuming that the functions at issue here are within that class, we may derive some of the properties of the first-order low-pass filter, as defined on the complex plane.

For one thing, if the original real functions are continuous, then according to the classification introduced in [2] the original inner analytic function has dominant singularities that are soft, with any degree of softness starting from borderline soft singularities (that is, with degree of softness zero), and the DP Fourier series are absolutely and uniformly convergent. In this case the action of the filter results in an inner analytic function with dominant singularities that have a degree of softness equal to $1$ or larger, thus implying that the corresponding filtered real functions are differentiable. We thus reproduce in the complex formalism one of the properties of the first-order filter [5], namely that if a real function is continuous then the corresponding filtered function is differentiable.

In addition to this, if the original real functions are integrable but not continuous, then according to the classification introduced in [2] the original inner analytic function has dominant singularities that are borderline hard ones (that is, with degree of hardness zero), and the DP Fourier series are convergent almost everywhere, but not absolutely or uniformly convergent. In this case the action of the filter results in an inner analytic function with dominant singularities which are borderline soft, thus implying that the corresponding filtered real functions are continuous. Also, in this case the filtered DP Fourier series become absolutely and uniformly convergent. We thus reproduce in the complex formalism another one of the properties of the first-order filter [6], namely that if a real function is discontinuous then the corresponding filtered function is continuous.

Since the filter acts only on the variable $\theta$, some of the properties of the filter defined on the real line, and hence on the unit circle, are translated transparently to the complex formalism. For example, the action on the filter on the Fourier expansions encoded into the angular part of the complex Taylor expansions is determined by its action on the elements of the Fourier basis, as shown in [10,11]. If we apply the filter as defined in Equation (4) to the functions of the basis we get

$$\begin{eqnarray*} \frac{1}{2\epsilon} \int_{\theta-\epsilon}^{\theta+\epsilon}... ...t[ \frac{\sin(k\epsilon)}{(k\epsilon)} \right] \sin(k\theta). \end{eqnarray*}$$

This means that the elements of that basis are eigenfunctions of the filter, interpreted as an operator. It also determines the eigenvalues, given by the ratio shown within brackets, which is known as the sinc function of the variable $(k\epsilon)$. What this means is that the filter acts of an extremely simple way on the Fourier expansions. It then follows that the same is true, of course, for the Taylor series of the corresponding inner analytic functions. If we write the Taylor expansion of a given inner analytic function in polar coordinates, with $z=\rho\exp(\mbox{\boldmath$\imath$}\theta)$, we get

$$w(z) = \sum_{k=1}^{\infty} a_{k} \rho^{k} \left[ \cos(k\theta) + \mbox{\boldmath$\imath$} \sin(k\theta) \right],$$

and from this follows at once the corresponding expansion for the filtered function

$$w_{\epsilon}(z) = \sum_{k=1}^{\infty} a_{k} \left[ \fr... ...k\theta) + \mbox{\boldmath$\imath$} \sin(k\theta) \right].$$

What this means is that the Taylor coefficients $a_{\epsilon ,k}$ of $w_{\epsilon }(z)$ are given by

$$a_{\epsilon,k} = \left[ \frac{\sin(k\epsilon)}{(k\epsilon)} \right] a_{k},$$

in terms of the Taylor coefficients $a_{k}$ of $w(z)$, a fact that can be shown directly from the definition of the coefficients, as one can see in Section A.1 of Appendix A. If we take the $\rho\to 1$ limit this corresponds to the filtered real functions

$$\begin{eqnarray*} f_{\epsilon,{\rm c}}(\theta) & = & \sum_{k=1}^{\infty} a_{... ...t[ \frac{\sin(k\epsilon)}{(k\epsilon)} \right] \sin(k\theta). \end{eqnarray*}$$

It follows therefore that the same relation holds for the Fourier coefficients of $f_{\epsilon,{\rm c}}(\theta)$ and $f_{\epsilon,{\rm s}}(\theta)$, in terms of the Fourier coefficients of $f_{\rm c}(\theta)$ and $f_{\rm s}(\theta)$.

Figure 2: The iteration of the first-order filter to produce an order-$N$ filter, showing the structure of the Pascal triangle and the linear increase of the range. The original singularity is at $\theta '$. The numbers near the vertices of the triangles represent the number of softened singularities superposed at that point.