Direct Derivation of the Coefficients $a_{\epsilon ,k}$

Let us determine the effect of the first-order linear low-pass filter, defined on the complex plane, on the coefficients $a_{k}$. We start with the Taylor coefficients of $w(z)$, which can be written in terms of its real an imaginary parts,

$$w(z) = f_{\rm c}(\rho,\theta)+\mbox{\boldmath$\imath$}f_{\rm s}(\rho,\theta),$$

in terms of which the Taylor coefficients are given by

$$\begin{eqnarray*} a_{k} & = & \frac{\rho^{-k}}{\pi} \int_{-\pi}^{\pi}d\theta... ...nt_{-\pi}^{\pi}d\theta\, f_{\rm s}(\rho,\theta) \sin(k\theta). \end{eqnarray*}$$

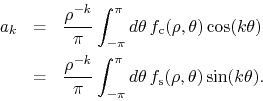
The Taylor coefficients of $w_{\epsilon }(z)$ are similarly given by

$$\begin{eqnarray*} a_{\epsilon,k} & = & \frac{\rho^{-k}}{\pi} \int_{-\pi}^{\p... ...\pi}d\theta\, f_{\epsilon,{\rm s}}(\rho,\theta) \sin(k\theta). \end{eqnarray*}$$

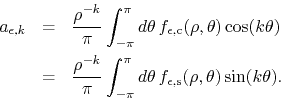
Let us work out only the first case, involving the cosine, since the work for the second one in essentially identical and leads to the same result. Using the definition of $f_{\epsilon,{\rm c}}(\rho,\theta)$ in terms of $f_{\rm c}(\rho,\theta)$ we have

$$\begin{eqnarray*} a_{\epsilon,k} & = & \frac{\rho^{-k}}{\pi} \int_{-\pi}^{\p... ...^{\pi}d\theta\, \sin(k\theta) f_{\rm c}(\rho,\theta-\epsilon), \end{eqnarray*}$$

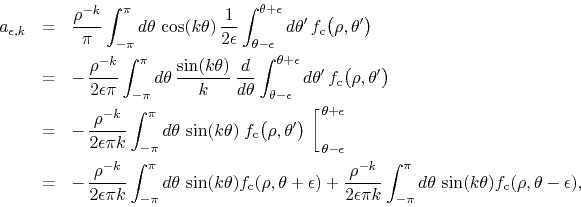
where we integrated by parts and where there is no integrated term due to the periodicity of the integrand in $\theta$. We now change variables in each integral, using $\theta'=\theta\pm\epsilon$, in order to obtain

$$\begin{eqnarray*} a_{\epsilon,k} & = & -\, \frac{\rho^{-k}}{2\epsilon \pi k}... ...silon\right) - \sin\!\left(k\theta'-k\epsilon\right) \right], \end{eqnarray*}$$

where the integration limits did not change in the transformations of variables due to the periodicity of the integrand. Changing $\theta '$ back to $\theta$ we are left with

$$\begin{eqnarray*} a_{\epsilon,k} & = & \frac{\rho^{-k}}{2\epsilon \pi k} \in... ...i}d\theta\, f_{\rm c}\!\left(\rho,\theta\right) \cos(k\theta). \end{eqnarray*}$$

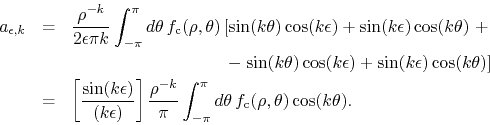
Since we recover in this way the expression of the coefficients of $f_{\rm c}(\rho,\theta)$, we get

$$a_{\epsilon,k} = \left[ \frac{\sin(k\epsilon)}{(k\epsilon)} \right] a_{k},$$

which is the same result obtained in the text through the application of the filter, as an operator, to the expansion of $w(z)$. This more direct derivation bypasses any preoccupations with the convergence of the series during that process, due to the term-wise application of the integral operator.