Next: Proof of Analyticity of Up: Appendix: Technical Proofs Previous: Direct Derivation of the
Here we establish that
![]() is analytic by showing that its
real and imaginary parts satisfy the Cauchy-Riemann conditions. Consider
an inner analytic function
is analytic by showing that its
real and imaginary parts satisfy the Cauchy-Riemann conditions. Consider
an inner analytic function ![]() and the corresponding filtered function
within the open unit disk, with the real angular parameter
and the corresponding filtered function
within the open unit disk, with the real angular parameter
![]()
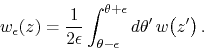
Since ![]() is analytic, we have
is analytic, we have
![]() where
where
![]() and
and
![]() satisfy the Cauchy-Riemann conditions in polar
coordinates,
satisfy the Cauchy-Riemann conditions in polar
coordinates,
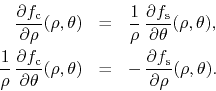
It follows that the filtered function can be written as
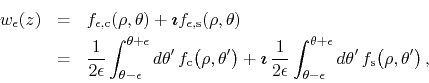
so that we have
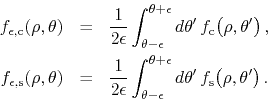
Since
![]() and
and
![]() are continuous
and differentiable, it is clear that so are
are continuous
and differentiable, it is clear that so are
![]() and
and
![]() . If we
calculate their partial derivatives with respect to
. If we
calculate their partial derivatives with respect to ![]() we get
we get
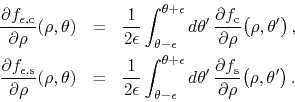
Using the Cauchy-Riemann relations for ![]() we may write these as
we may write these as
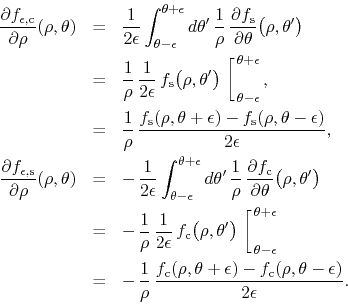
If we now calculate the partial derivatives of
![]() and
and
![]() with respect
to
with respect
to ![]() we get
we get
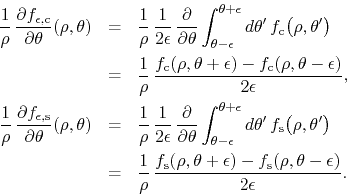
Comparing this pair of equations with the previous one we get
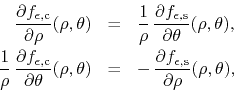
which establish the analyticity of
![]() , in the same domain
as that of
, in the same domain
as that of ![]() . Let us now examine the other properties defining an
inner analytic function. For one thing we have
. Let us now examine the other properties defining an
inner analytic function. For one thing we have ![]() , which means that
, which means that
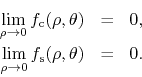
If we calculate the corresponding limits for
![]() we get
we get
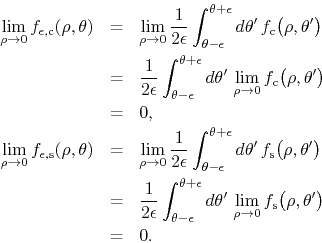
We have therefore that
![]() . Finally,
. Finally, ![]() reduces to a
real function over the interval
reduces to a
real function over the interval ![]() of the real axis, which means
that its imaginary part is zero there, and therefore that
of the real axis, which means
that its imaginary part is zero there, and therefore that
![]() and
and
![]() . If we write
. If we write
![]() for the same values of
for the same values of ![]() we get
we get
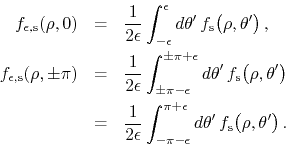
However, since ![]() is an inner analytic function we have that
is an inner analytic function we have that
![]() is an odd function of
is an odd function of ![]() . In both cases above
this implies that the integral is zero, and hence we conclude that
. In both cases above
this implies that the integral is zero, and hence we conclude that
![]() is an inner analytic function as well.
is an inner analytic function as well.