The Infinite-Order Filter

Let us now discuss the possibility of constructing infinite-order filters with compact support. As was mentioned before, it would be an interesting thing to have the definition of an infinite-order linear low-pass filter. If we consider the linear low-pass filter of order $N$ and a fixed range $\epsilon$, that can be described in terms of the inner-analytic functions as

$$w_{\epsilon}^{(N)}(z) = \left(\frac{-\mbox{\boldmath$\ima... ...[z\,{\rm e}^{\mbox{\boldmath$\imath$}(1-2n/N)\epsilon}\right],$$ (6)

it is natural to ask that happens if we take the $N\to \infty$ limit. This cannot be described simply as an infinite iteration of the first-order linear filter, since the limiting process changes the range of that filter to zero. On the other hand, all the filtered complex functions $w_{\epsilon}^{(N)}(z)$ exist and are inner analytic, as a sequence indexed by $N$, for all $N$, so that it is reasonable to think that the limit should also exist and should also be an inner analytic function, at least inside the open unit disk of the complex plane. However, it is important to keep in mind that it is far less clear what happens when one takes the limit from the open unit disk to the unit circle, after one first takes the $N\to \infty$ limit.

In this section we will endeavor to construct an infinite-order filter with compact support. If this endeavor succeeds, then there is an interesting consequence of the eventual construction of such an infinite-order filter, regarding the construction of $C^{\infty}$ functions with compact support. If it turns out to be possible to define this infinite-order filter with a finite range $\epsilon$ in terms of an integral involving a well-defined infinite-order kernel with compact support,

$$f_{\epsilon}^{(\infty)}(\theta) = \int_{-\pi}^{\pi}d\thet... ...\epsilon}^{(\infty)}\!\left(\theta-\theta'\right) f(\theta'),$$

then it would in principle be possible to use this filter operator to transform any integrable function into a $C^{\infty}$ function, making changes only within a finite range $\epsilon$ that can be as small as one wishes. In our current case here this infinite-order kernel would be written as the limit

$$\begin{eqnarray*} K_{\epsilon}^{(\infty)}\!\left(\theta-\theta'\right) & = & ... ...} \right]^{N} \cos\!\left[k\left(\theta-\theta'\right)\right]. \end{eqnarray*}$$

The idea here is that the kernel $K_{\epsilon}^{(\infty)}\!\left(\theta-\theta'\right)$ would then be itself a $C^{\infty}$ function, and that due to the properties of the first-order filter, it would also have unit integral. However, the fact is that the limit above does not behave as one might expect at first. If we consider the $N\to \infty$ limit of the coefficients, we have

$$\begin{eqnarray*} \lefteqn { \lim_{N\to\infty} \left[ \left(\frac{N}{k\epsi... ...} \left(\frac{k\epsilon}{N}\right)^{6} + \ldots \right]^{N}. \end{eqnarray*}$$

If one expands the power $N$, there is one term equal to $1$ and all other terms have powers of $N$ in the denominator. If we write the terms that have up to four powers of $N$ in the denominator, we get

$$\begin{eqnarray*} \lefteqn { \lim_{N\to\infty} \left[ \left(\frac{N}{k\epsi... ...(N-1) \left(\frac{k\epsilon}{N}\right)^{6} + \ldots \right]. \end{eqnarray*}$$

A more rigorous analysis of this limit would require more careful consideration of the convergence of this series, since in principle one must be careful with the interchange of the $N\to \infty$ limit and the $j\to\infty$ limit of the series. However, it turns out that this rough discussion suffices for our purposes here. As one can see, all terms except the first have at least one factor of $N$ in the denominator, and therefore we should expect that

$$\lim_{N\to\infty} \left[ \left(\frac{N}{k\epsilon}\right) \sin\!\left(\frac{k\epsilon}{N}\right) \right]^{N} = 1,$$

for all $k$. This implies that we have for the finite-range kernel, in the $N\to \infty$ limit,

$$\begin{eqnarray*} K_{\epsilon}^{(\infty)}\!\left(\theta-\theta'\right) & = & ... ...{k=1}^{\infty} \cos\!\left[k\left(\theta-\theta'\right)\right], \end{eqnarray*}$$

which is in fact the Fourier expansion of the Dirac delta ``function'', which is something of an unexpected outcome! In other words, the limit of this sequence of progressively smoother functions is not even a function, but a singular object instead. This is actually very similar to the representation of the delta ``function'' by an infinite sequence of normalized Gaussian functions.

Figure 3: The kernels of several filters with increasing range $N\epsilon$, obtained via the use of their Fourier series, for $\epsilon =0.5$, for values of $N$ increasing exponentially, in the set $\{1,2,4,8,16,32,64,128\}$, plotted as functions of $\left (\theta -\theta '\right )$ within the periodic interval $[-\pi ,\pi ]$.

A little numerical exploration is useful at this point to establish some simple mathematical facts about these infinite-order kernels. For completeness, let us go momentarily back to the straightforward multiple superposition of the first-order filter. If we take the $N\to \infty$ limit of the kernel of order $N$ with range $N\epsilon$, we might try to define a first infinite-order kernel with infinite range as

$$K_{\infty}^{(\infty)}\!\left(\theta-\theta'\right) = \fra... ... \right]^{N} \cos\!\left[k\left(\theta-\theta'\right)\right].$$

Figure 4: The kernels of several filters with constant range $\epsilon$, obtained via the use of their Fourier series, for $\epsilon =0.5$, for values of $N$ increasing exponentially, in the set $\{1,2,4,8,16,32, 64,128,256,512,1024,2048,4096,8192\}$, plotted as functions of $\left (\theta -\theta '\right )$ over a small sub-interval within the periodic interval $[-\pi ,\pi ]$.

Since this Fourier series converges very fast, and ever faster as $N$ increases, it is very easy to use it to plot the corresponding functions. Doing this one gets the sequence of functions shown in Figure 3. As expected, the range increases without bound and the kernel gets distributed more and more over the whole periodic interval, approaching a constant function with unit integral. This means that only the constant term of the Fourier expansion survives the limit, and that all the other Fourier coefficients converge to zero. There is nothing too surprising about this, since it is consistent with the fact that

$$\lim_{N\to\infty} \left[ \frac{\sin(k\epsilon)}{(k\epsilon)} \right]^{N} = 0,$$

so long as $\sin(k\epsilon)<(k\epsilon)$, which is true since $k>0$ and $\epsilon>0$. Once again a more rigorous analysis of this limit would require more careful consideration of the convergence of the series, since in principle one must be careful with the interchange of the $N\to \infty$ limit and the $k\to\infty$ limit of the series. However, here too it turns out that this rough discussion suffices for our purposes. It is quite clear that, if we could repeat the experiment on the whole real line instead of the periodic interval, the kernel would approach a normalized Gaussian function that in turn would approach zero everywhere, becoming ever wider and lower as $N\to \infty$.

Figure 5: The kernels of several filters with Gaussian range $\sqrt {N}\epsilon$, obtained via the use of their Fourier series, for $\epsilon =0.5$, for values of $N$ increasing exponentially, in the set $\{1,2,4,8,16,32,64,128,256,512,1024\}$, plotted as functions of $\left (\theta -\theta '\right )$ over a sub-interval within the periodic interval $[-\pi ,\pi ]$.

If we now consider once again the $N\to \infty$ limit of the kernel of order $N$ with constant range $\epsilon$, we might try to define an infinite-order kernel of finite range $\epsilon$ as

$$K_{\epsilon}^{(\infty)}\!\left(\theta-\theta'\right) = \f... ... \right]^{N} \cos\!\left[k\left(\theta-\theta'\right)\right].$$

Our previous analysis indicated that this has the delta ``function'' as its limit. Plotting this kernel one gets the sequence of functions shown in Figure 4. As one can see, the kernel in fact diverges to positive infinity at zero. It also seems to go to zero everywhere else. Since it still has constant integral, and since it can be easily verified that its maximum at zero diverges to infinity as $\sqrt{N}$, we must conclude that it in fact approaches a Dirac delta ``function''. More precisely, the sequence of kernels approaches a normalized Gaussian function that in turns approaches the delta ``function'', becoming ever taller and narrower as $N\to \infty$, with constant area under the graph. What we have here is a singular limit, in a way going full circle, from the delta ``function'' at $N=0$ and back to it at $N\to \infty$. Therefore the $N\to \infty$ limit of this order-$N$ kernel is not a $C^{\infty}$ function, but a singular object instead, which is certainly an unexpected and surprising result.

This suggests that one may take an intermediate limit, which perhaps will converge to a non-singular localized function, by superposing $N$ filters with range $\sqrt {N}\epsilon$, thus obtaining a second infinite-order kernel with infinite range, given by

$$K_{\infty}^{(\infty)}\!\left(\theta-\theta'\right) = \fra... ... \right]^{N} \cos\!\left[k\left(\theta-\theta'\right)\right].$$

In fact, this exercise results in the sequence of functions seen in Figure 5, which approaches very fast a function very similar to a normalized Gaussian function with finite and non-zero width. Again it is quite clear that, if we could repeat this construction on the whole real line, then the limit would be a normalized Gaussian function, but in our case here it is a bit deformed by its containment within the periodic interval. When its width is small when compared to the length $2\pi$ of the periodic interval the Gaussian approaches zero very fast when we go significantly away from its point of maximum, so that we may consider this case to be paracompact, and even use this filter successfully in the practice of physics applications. However, the exact mathematical fact is that the range of this filter does tend to infinity when $N\to \infty$, and therefore to the whole extent of the periodic interval, if we execute all this operation within it.

It is possible to interpret qualitatively what happens in these three cases in terms of the expression for the corresponding superpositions of inner analytic functions. In the case of the straight multiple superposition of the first-order kernel we have for the representation of the order-$N$ filter on the complex plane

$$w_{N\epsilon}^{(N)}(z) = \left(\frac{-\mbox{\boldmath$\im... ...ft(z\,{\rm e}^{\mbox{\boldmath$\imath$}[N-2n]\epsilon}\right),$$

where we may assume that the coefficients do not diverge with $N$, since the function tends to a constant everywhere on the unit circle in the $N\to \infty$ limit. In the case of the superposition of the first-order kernel with decreasing range $\epsilon/N$, resulting on a fixed range $\epsilon$ for the order-$N$ kernel, the representation of the order-$N$ filter in the complex plane is

$$w_{\epsilon}^{(N)}(z) = \left(\frac{-\mbox{\boldmath$\ima... ...(z\,{\rm e}^{\mbox{\boldmath$\imath$}[1-2n/N]\epsilon}\right),$$

so that the extra factor of $N^{N}$ is clearly related to the divergence at a point on the unit circle, when we make $N\to \infty$. In the case of the superposition of the first-order kernel with decreasing range $\epsilon/\sqrt{N}$, resulting on a range $\sqrt {N}\epsilon$ for the order-$N$ kernel, the representation of the order-$N$ filter in the complex plane is

$$w_{\sqrt{N}\epsilon}^{(N)}(z) = \left(\frac{-\mbox{\boldm... ...ath$\imath$}\left[\sqrt{N}-2n/\sqrt{N}\right]\epsilon}\right).$$

Note that in this case we gained a factor of $N^{N/2}$ rather than $N^{N}$, which the consequence that over the unit circle the kernel neither approaches a constant everywhere nor diverges to infinity somewhere. In this case the coefficients seem to have well-defined finite limits.

We must therefore conclude that, with this type of multiple superposition of the first-order filter, and the corresponding superposition of the singularities of the inner analytic functions in the complex plane, we are unable to define an infinite-order kernel that is both a finite and smooth real function, and that at the same time is localized within a compact support, thus generating an infinite-order filter with a finite range $\epsilon$. In order to understand why, it is useful to look at the singularities, on the unit circle of the complex plane, of the sequence of inner analytic functions generated by the repeated application of the first-order filter, starting with the inner analytic function corresponding to the zero-order kernel, which is a Dirac delta ``function'' and thus has a single first-order pole at some point on the unit circle, as shown in [1].

If we look at the diagram in Figure 2, we see that as the multiple application of the first-order filter goes on, more and more softened singularities are superposed at the points near the center of the diagram. Each singularity is progressively softer, but they are superposed in increasing numbers, thus generating a coefficient in the corresponding term in the superposition shown in Equation (6). For each finite $N$ these coefficients may be large, but they are finite, and therefore they do not disturb the softness of the corresponding singularities. However, if one of the coefficients diverges in the $N\to \infty$ limit, then the corresponding singularity is no longer soft in the limit. Let us recall that the definition of a soft singularity, as given in [2], is that the limit of the inner analytic function to that point be finite. Because of the diverging coefficients, in this type of superposition this may fail to be so in the $N\to \infty$ limit, even if the singularities are soft for each finite value of $N$.

Figure 6: The scaled iteration of the first-order filter to produce an order-$N$ filter, showing the range $\epsilon _{N}$ tending to the limit $\epsilon$. The original singularity is at $\theta '$. The numbers near the vertices of the triangles show that there is just one softened singularity at each such point.

We are therefore led to the idea of changing the method of iteration of the first-order filters in such a way that the softened singularities never get superposed. It is not too difficult to see that one may accomplish this by superposing filters with progressively smaller ranges, as illustrated by the diagram in Figure 6. Given a value of $\epsilon$, this diagram corresponds to a process in which we start by applying the first-order filter with range $\epsilon/2$, followed by the first-order filter of range $\epsilon/4$, then by the filter of range $\epsilon/8$, and so on, where the range of the $N^{\rm th}$ filter applied is given by $\epsilon/2^{N}$. Note that at the $N^{\rm th}$ iteration there are $2^{N}$ singularities homogeneously distributed within the interval $(-\epsilon,\epsilon)$. Since the ranges are scaled down exponentially, we call this a scaled filter, and the corresponding kernel a scaled kernel.

Figure 7: The kernels of several scaled filters with range $\epsilon _{N}\to \epsilon$, obtained via the use of their Fourier series, for $\epsilon =0.5$, for values of $N$ increasing linearly, in the set $\{1,2,3,4,5,6,7,8,9,10\}$, plotted as functions of $\left (\theta -\theta '\right )$ over the support interval $[-\epsilon ,\epsilon ]$. The dashed lines mark the ends of the support interval.

At the $N^{\rm th}$ iteration there are $2^{N}$ singularities, each one softened by $N$ degrees, spaced from one another by $\epsilon/2^{N-1}$, and spaced from the ends of the $[-\epsilon ,\epsilon ]$ interval by $\epsilon/2^{N}$. They are, therefore, regularly distributed within the interval $(-\epsilon,\epsilon)$, centered at $2^{N}$ consecutive sub-intervals of length $\epsilon/2^{N-1}$. In the $N\to \infty$ limit the singularities will tend to become homogeneously distributed within the interval $(-\epsilon,\epsilon)$, and indeed will tend to a countable infinity of infinitely soft singularities distributed densely within that interval. Since at the $N^{\rm th}$ step there are $2^{N}$ such singularities, we see that their number grows exponentially fast. However, the singularities never get superposed. The corresponding superposition in terms of inner analytic functions in the complex plane is given by

$$\begin{eqnarray*} \bar{w}_{\epsilon_{N}}^{(N)}(z) & = & \left(\frac{-2^{1}\mb... ...x{\boldmath$\imath$}\left[1-(2n-1)/2^{N}\right]\epsilon}\right). \end{eqnarray*}$$

Using the property of the first-order filter regarding its action on Fourier expansions [10,11], it is not difficult to write the Fourier expansion of this new scaled kernel, at the $N^{\rm th}$ step of the construction process, which has a range $\epsilon _{N}$ such that $\epsilon/2\leq \epsilon_{N}<\epsilon$,

$$\bar{K}_{\epsilon_{N}}^{(N)}\!\left(\theta-\theta'\right) ... ...t)} \right] \cos\!\left[k\left(\theta-\theta'\right)\right],$$

where the coefficients include a product of $N$ different sinc factors. This product can be written as

$$\begin{eqnarray*} \left[ \frac {\sin\!\left(k\epsilon/2^{1}\right)} {\left(k... ...}} \prod_{n=1}^{N} \sin\!\left(\frac{k\epsilon}{2^{n}}\right). \end{eqnarray*}$$

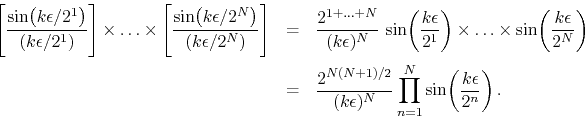
It follows that we have for this order-$N$ scaled kernel

$$\bar{K}_{\epsilon_{N}}^{(N)}\!\left(\theta-\theta'\right) ... ...ht) \right] \cos\!\left[k\left(\theta-\theta'\right)\right].$$ (7)

As expected, this kernel indeed has a well-defined limit when $N\to \infty$, with support in the finite interval $\left[\theta'-\epsilon,\theta'+\epsilon\right]$, as one can see in the graph of Figure 7. The sequence of kernels converges exponentially fast to a definite function, with a rather unusual shape.

Figure 8: The best approximation of the kernel of the scaled filter with constant range $\epsilon$, in the $N\to \infty$ limit, obtained via the use of its Fourier series, for $\epsilon =0.5$, for a large value of $N$ ($100$), plotted as a function of $\left (\theta -\theta '\right )$ over the support interval $[-\epsilon ,\epsilon ]$. The dashed lines mark the ends of the support interval.

It is possible to demonstrate explicitly the convergence of the sequence of scaled kernels $\bar{K}_{\epsilon_{N}}^{(N)}\!\left(\theta-\theta'\right)$ to a well-defined regular function $\bar{K}_{\epsilon}^{(\infty)}\!\left(\theta-\theta'\right)$ in the $N\to \infty$ limit. The proof is rather lengthy and is presented in full in Appendix B. It depends on the following facts about this limit, that we may establish here in order to give a general idea of the structure of the proof. First of all, due to one of the properties of the first-order filter [8] all kernels in the sequence have unit integral. Second, the range $\epsilon _{N}$ of the order-$N$ kernel is given by the combined ranges of all the kernels used to build it, and is therefore given by

$$\epsilon_{N} = \frac{\epsilon}{2} + \frac{\epsilon}{4} ... ...ldots + \frac{\epsilon}{2^{N-1}} + \frac{\epsilon}{2^{N}},$$

which is a geometric progression with ratio $1/2$. We have therefore

$$\begin{eqnarray*} \epsilon_{N} & = & \epsilon\, \frac { {\displaystyle\fra... ...}} } \\ & = & \epsilon \left( 1-\frac{1}{2^{N}} \right). \end{eqnarray*}$$

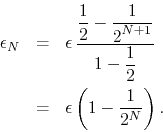
It follows therefore that in the $N\to \infty$ limit $\epsilon _{N}$ tends to $\epsilon$,

$$\lim_{N\to\infty}\epsilon_{N} = \epsilon.$$

Therefore all the kernels in the sequence remain identically zero everywhere outside the interval $(-\epsilon,\epsilon)$, so that we may conclude that the limiting function has support within that interval. Next we observe that, since the filtered function is defined as an average of the original function, it can never assume values which are larger than the maximum of the function it is applied on, or smaller than its minimum. Therefore, since the first kernel we start with, with range $\epsilon/2$, is limited within the interval $[0,1/\epsilon]$, so are all the subsequent kernels of the construction sequence.

As a consequence all these considerations, the non-zero parts of the graphs of all the kernels in the construction sequence are contained within the rectangle defined by the support interval $[-\epsilon ,\epsilon ]$ and the range of values $[0,1/\epsilon]$, which has area $2$. The area of the graph of every kernel in the construction sequence is $1$, so that it occupies one half of the area of the rectangle. Since every scaled kernel in the construction sequence is a continuous and differentiable function, it becomes clear that the $N\to \infty$ limit of the sequence of kernels must also be a regular function within this rectangle. It follows from the discussion in Appendix B that the limit of the sequence exists and is a regular, continuous and differentiable function, resulting in the infinite-order scaled kernel with range $\epsilon$

$$\bar{K}_{\epsilon}^{(\infty)}\!\left(\theta-\theta'\right) ... ...y} \bar{K}_{\epsilon_{N}}^{(N)}\!\left(\theta-\theta'\right).$$

This infinite-order scaled kernel has the deceptively simple look shown in Figure 8. Despite appearances it contains no completely straight segments within its support interval. Once it is shown that it is a $C^{\infty}$ function, it follows that its derivatives of all orders are zero at the two extremes of the support interval, where they must match the correspondingly zero derivatives of the two external segments, on either side of the support interval, where the kernel is identically zero.

A technical note about the graphs representing the $N\to \infty$ limit of various quantities is in order at this point. They were obtained numerically from the corresponding Fourier series, using the scaled filter of order $N=100$. This means that the last first-order filter used in the multiple superposition has a range of $\epsilon/2^{100}$. This is less than $\epsilon/10^{30}$ and is therefore many orders of magnitude below any graphical resolution one might hope for, in any medium. Certainly the errors related to the summation of the Fourier series, which were set at $10^{-12}$, are the dominant ones, but still extremely small. We may conclude that these graphs are faithful representations of the corresponding quantities for all conceivable graphical purposes. The programs used in creating all the graphs shown in this paper are freely available online [12].

It is quite simple to see that this kernel is a $C^{\infty}$ function. Its Fourier series, given as the $N\to \infty$ limit of the Fourier expansion in Equation (7), is certainly absolutely and uniformly convergent, and any finite-order term-wise derivative of it results in another series with the same properties. Since the convergence of the resulting series is the additional condition, besides uniform convergence, that suffices to guarantee that one can differentiate the series term-wise in order to obtain the derivative of the function, we may conclude that derivatives of all finite orders exist and are given by continuous and differentiable functions. This proof of infinite differentiability of the $\bar{K}_{\epsilon}^{(\infty)}\!\left(\theta-\theta'\right)$ kernel now ensures that the kernel and all its multiple derivatives are in fact zero at the points $\left(\theta-\theta'\right)=\pm\epsilon$.

An independent discussion of the existence of the derivatives of all finite orders can be found in Section B.7 of Appendix B. There one can see also that the derivatives of all orders are zero at the central point of maximum, as well as at the two extremes of the support interval. We also show in Section B.8 of Appendix B that the infinite-order scaled kernel is not analytic as a function on the periodic interval, in the real sense of the term. We do this by showing that there is a countable infinity of points, distributed densely in the support interval, where only a finite number of derivatives is different from zero. We also discuss briefly there the question of whether or not the infinite-order scaled kernel can be extended analytically to the complex plane. We discuss this in terms of the fact that it is the limit of an inner analytic function when one takes the limit to the border of the unit disk.

Figure 9: The filtered square wave and the parameters related to the action of the infinite-order scaled filter, obtained via the use of its Fourier series, for $\epsilon =0.5$, for a large value of $N$ ($100$), plotted as a function of $\theta$ over the periodic interval $[-\pi ,\pi ]$. The original function is shown with the dashed line and the filtered function with the solid line. The dotted lines mark the intervals where the function was changed by the filter.

Given that the infinite-order scaled kernel is a $C^{\infty}$ function, one may then define an infinite-order filter based on this infinite-order scaled kernel. However, in this case it is not so simple to determine the form of the coefficients directly in the $N\to \infty$ limit. In fact, the question of whether or not it is possible to write the coefficients directly in the $N\to \infty$ limit, in some simple form, is an open one. Note that, as was mentioned before, one must be careful with the interchange of the $N\to \infty$ limit and the $k\to\infty$ limit of the series. In any case, it follows that given any merely integrable function $f(\theta)$, the filtered function

$$f_{\epsilon}^{(\infty)}(\theta) = \int_{-\infty}^{\infty}... ...infty)}\!\left(\theta-\theta'\right) f\!\left(\theta'\right),$$

is necessarily a $C^{\infty}$ function, in the real sense of the term. It is easy to see this, since the differentiations with respect to $\theta$ at the right-hand side will act only on the infinite-order scaled kernel, which is a $C^{\infty}$ function. Therefore all the finite-order derivatives of $f_{\epsilon}^{(\infty)}(\theta)$ exist, since they may be written as

$$\frac{d^{n}}{d\theta^{n}} f_{\epsilon}^{(\infty)}(\theta) ... ...\left(\theta-\theta'\right) \right] f\!\left(\theta'\right),$$

where the $n^{\rm th}$ derivative of the infinite-order scaled kernel is a limited, continuous and differentiable function with compact support, being therefore an integrable function. In addition to this, the changes made in $f(\theta)$ in order to produce $f_{\epsilon}^{(\infty)}(\theta)$ have a finite range $\epsilon$ that can be made as small as one wishes.

Figure 10: The filtered sawtooth wave wave and the parameters related to the action of the infinite-order scaled filter, obtained via the use of its Fourier series, for $\epsilon =0.5$, for a large value of $N$ ($100$), plotted as a function of $\theta$ over the periodic interval $[-\pi ,\pi ]$. The original function is shown with the dashed line and the filtered function with the solid line. The dotted lines mark the intervals where the function was changed by the filter.

Let us now consider the action of such a filter on inner analytic functions. There is no difficulty in determining what happens to the singularities of the inner analytic functions on the unit circle, as a consequence of the application of this infinite-order scaled filter. It is quite clear that a single singularity of the inner analytic function at $\theta$ would be smeared into a denumerable infinity of softened singularities within the interval $[\theta-\epsilon,\theta+\epsilon]$ on the unit circle. This set of singularities would occupy the interval densely, and they would be infinitely soft, since they are the result of an infinite sequence of logarithmic integrations. Since each logarithmic integration renders the real function on the unit circle differentiable to one more order, in the limit one gets over that circle an infinitely differentiable real function of $\theta$. So the resulting complex function of $z$ must be an inner analytic function which has only infinitely soft singularities on the unit circle and that is a $C^{\infty}$ function of $\theta$ when restricted to that circle. The same is true for the kernel itself, if we start with a single first-order pole at $\theta$, which is the case for the order-zero kernel. Note that in either case this real function is $C^{\infty}$ right on top of a densely-distributed set of singularities of the corresponding inner analytic function, which is somewhat unexpected, even if they are infinitely soft singularities.

As a simple example, let us consider the unit-amplitude square wave, which is a discontinuous periodic function, as one can see in Figure 9, that shows the filtered function superposed with the original one. The filtered function was obtained from its Fourier series, which due to the properties of the first-order filter is easily obtained, being given by

$$f_{\epsilon_{N}}(\theta) = \frac{4}{\pi} \sum_{j=0}^{\in... ...k\epsilon}{2^{n}}\right) \right] \sin\!\left(k\theta\right),$$

where $k=2j+1$, for a large value of $N$. The graph of the original function has two straight horizontal segments and two points of discontinuity at $\theta=0$ and at $\theta=\pm\pi$. It follows that the corresponding inner analytic function has two borderline hard singularities at these two points. Let us consider all the instances of the first-order linear low-pass filter used for the construction of the infinite-order scaled kernel, for all construction steps $N$ and any value of $\epsilon<\pi$. Since the linear low-pass filters are all the identity on the segments that are linear functions, up to a distance of $\epsilon$ to one of the singularities, the function would never be changed at all outside the two intervals $[-\epsilon ,\epsilon ]$ and $[\pi-\epsilon,-\pi+\epsilon]$, when one applies to it any of the order-$N$ scaled filters. After the end of the process of application of the infinite-order scaled filter these two intervals would contain segments of $C^{\infty}$ functions of $\theta$, and in fact the whole resulting function would be a $C^{\infty}$ function of $\theta$, over the whole unit circle.

Figure 11: The filtered triangular wave and the parameters related to the action of the infinite-order scaled filter, obtained via the use of its Fourier series, for $\epsilon =0.5$, for a large value of $N$ ($100$), plotted as a function of $\theta$ over the periodic interval $[-\pi ,\pi ]$. The original function is shown with the dashed line and the filtered function with the solid line. The dotted lines mark the intervals where the function was changed by the filter.

Another similar example can be seen in Figure 10, which shows the case of the unit-amplitude sawtooth wave, which also has the same two points of discontinuity and therefore corresponds to an inner analytic function with two similar borderline hard singularities at these points. The filtered function was obtained from its Fourier series,

$$f_{\epsilon_{N}}(\theta) = -\, \frac{4}{\pi} \sum_{j=1}... ...k\epsilon}{2^{n}}\right) \right] \sin\!\left(k\theta\right),$$

where $k=2j$, for a large value of $N$. In Figure 11 one can see the case of the triangular wave, which is a continuous function with two points of non-differentiability at $\theta=0$ and at $\theta=\pm\pi$, and therefore corresponds to an inner analytic function with two borderline soft singularities at these points. The filtered function was obtained from its Fourier series,

$$f_{\epsilon_{N}}(\theta) = -\, \frac{8}{\pi^{2}} \sum_{... ...k\epsilon}{2^{n}}\right) \right] \cos\!\left(k\theta\right),$$

where $k=2j+1$, for a large value of $N$. In all cases we chose a rather large value for $\epsilon$ as compared to its maximum value $\pi$, namely $0.5$, in order to render the action of the scaled infinite-order filter clearly visible. What we seem to have here is a factory of $C^{\infty}$ functions of $\theta$ on the unit circle. Starting with virtually any integrable function, we may consider the application of the infinite-order scaled filter in order to produce a $C^{\infty}$ function on the unit circle, making changes only with a range $\epsilon$ that can be as small as we wish.

Once we have the infinite-order scaled filter defined within the periodic interval, it is simple to extend it to the whole real line. Considering that the infinite-order scaled kernel and all its derivatives are zero at the two ends of its support interval, we may just take that support interval and insert it into the real line. If we make the new infinite-order scaled kernel identically zero outside the support interval, in all the rest of the real line, we still have a $C^{\infty}$ function. This is so because at the two points of concatenation the two lateral limits of the kernel are equal, being both zero, as are the two lateral limits of its first derivative, and the same for all the higher-order derivatives. Therefore, we may also define an infinite-order scaled filter acting on the whole real line, that maps any integrable real function to corresponding $C^{\infty}$ functions.