Next: Invariance of the Sign Up: Proof of Convergence to Previous: Proof of Convergence to
According to one of the properties established before for the first-order
filter [5], if ![]() is continuous in the domain where
the filter is applied, then
is continuous in the domain where
the filter is applied, then
![]() is differentiable, and
its derivative is given by
is differentiable, and
its derivative is given by
This is valid so long as the support interval of the filter fits
completely inside the region where ![]() is continuous. This
immediately implies that, in a region where
is continuous. This
immediately implies that, in a region where ![]() increases
monotonically we have
increases
monotonically we have
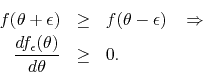
We may therefore conclude that
![]() also increases
monotonically within the sub-region where the support interval of the
filter fits inside the region in which
also increases
monotonically within the sub-region where the support interval of the
filter fits inside the region in which ![]() is continuous. In the
same way, in a region where
is continuous. In the
same way, in a region where ![]() decreases monotonically we have
decreases monotonically we have
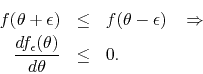
We may therefore conclude that
![]() also decreases
monotonically within that same sub-region. In other words, the monotonic
character of the variation of a function is invariant by the action of the
filter. In particular, at points where
also decreases
monotonically within that same sub-region. In other words, the monotonic
character of the variation of a function is invariant by the action of the
filter. In particular, at points where ![]() is differentiable the
sign of its derivative is invariant by the action of the filter.
is differentiable the
sign of its derivative is invariant by the action of the filter.