Como já observamos no início deste capítulo, em um plasma
carregado em ![]() dimensões, o potencial entre duas cargas estáticas separadas
por uma distância
dimensões, o potencial entre duas cargas estáticas separadas
por uma distância ![]() é dado pela Eq. (3.26), ou
seja,
é dado pela Eq. (3.26), ou
seja,
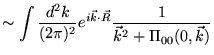 |
|||
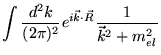 |
|||
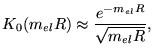 |
(3.80) |
onde ![]() é a função de Bessel modificada
e
é a função de Bessel modificada
e ![]() é a massa elétrica. Nesta seção vamos calcular, a
um laço,
é a massa elétrica. Nesta seção vamos calcular, a
um laço, ![]() para os modelos Maxwell-Chern-Simons-Higgs e
QED com um termo de Chern-Simons em
para os modelos Maxwell-Chern-Simons-Higgs e
QED com um termo de Chern-Simons em ![]() dimensões.
dimensões.
Inicialmente iremos calcular explicitamente o propagador completo do
campo de calibre no caso escalar. Como já foi visto anteriormente ,
Eq. (3.29), o campo de calibre adquire, já na
aproximação de árvore, dois pólos massivos com massas
![]() . Se quisermos adicionar a ele as contribuições
provenientes da auto-energia do fóton, temos [26]:
. Se quisermos adicionar a ele as contribuições
provenientes da auto-energia do fóton, temos [26]:
com
e
Assim, a inclusão de correções radiativas, a priori,
preserva a estrutura de duas massas para o campo de calibre, agora
![]() ao invés de
ao invés de ![]() . Colecionando os resultados obtidos
para os fatores de forma no limite estático, Eq. (3.71)
podemos calcular
. Colecionando os resultados obtidos
para os fatores de forma no limite estático, Eq. (3.71)
podemos calcular ![]() ,
, ![]() e
e ![]() como sendo:
como sendo:
| (3.83) |
| (3.84) |
e
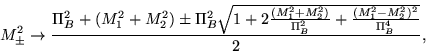 |
(3.85) |
levando a:
| (3.86) |
e
| (3.87) |
Unindo estes resultados, podemos obter ![]() de (3.92)
como:
de (3.92)
como:
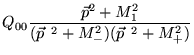 |
|||
![$\displaystyle Q_{00} \left[ \frac{M_+^2 - M_1^2}{M_+^2 - M_-^2}
\frac{1}{\vec{p...
...{M_-^2 - M_1^2}{M_+^2 - M_-^2}
\frac{1}{\vec{p}^{\phantom a 2} + M_-^2} \right]$](img483.png) |
|||
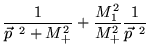 |
|||
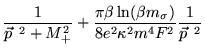 |
|||
| (3.88) |
e de maneira análoga, chegamos a:
| (3.89) |
Concluímos deste resultado que, embora na forma geral
do propagador completo do campo de calibre apareçam duas massas, a
um laço, limite estático e regime de altas temperaturas,
somente uma delas sobrevive tanto em ![]() quanto em
quanto em ![]() e
podemos identificá-las trivialmente com as
e
podemos identificá-las trivialmente com as ![]() e
e ![]() ,
respectivamente. Note que aqui, em contraste com o caso
quadridimensional, a massa magnética não é nula.
,
respectivamente. Note que aqui, em contraste com o caso
quadridimensional, a massa magnética não é nula.
Para a ![]() , o propagador completo é obtido como sendo:
, o propagador completo é obtido como sendo:
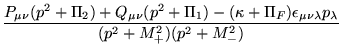 |
|||
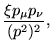 |
(3.90) |
onde ![]() são as mesmas massas do caso escalar,
Eq. (3.93), com
são as mesmas massas do caso escalar,
Eq. (3.93), com
![]() e
e
![]() . Vale salientar que no caso fermiônico, embora na
aproximação de árvore haja somente um pólo massivo, como
podemos observar na Eq. (3.82), quando incorporamos a
este resultado as correções radiativas, chegamos à mesma
estrutura de duas massas do caso bosônico. Neste caso, substituindo
os valores de
. Vale salientar que no caso fermiônico, embora na
aproximação de árvore haja somente um pólo massivo, como
podemos observar na Eq. (3.82), quando incorporamos a
este resultado as correções radiativas, chegamos à mesma
estrutura de duas massas do caso bosônico. Neste caso, substituindo
os valores de ![]() e
e ![]() obtidos no limite estático,
Eq. (3.90), temos que:
obtidos no limite estático,
Eq. (3.90), temos que:
| (3.91) |
| (3.92) |
e
| (3.93) |
onde ![]() é definido a partir da
Eq. (3.86). Dos resultados acima chegamos a
é definido a partir da
Eq. (3.86). Dos resultados acima chegamos a
| (3.94) |
| (3.95) |
o que implica nas seguinte componentes de ![]()
| (3.96) |
e
![$\displaystyle P_{ii}\left[ \frac{M_+^2 - M_2^2}{M_+^2 -
M_-^2}\frac{1}{\vec{p}^...
...ac{M_-^2 - M_2^2}{M_+^2 -
M_-^2}\frac{1}{\vec{p}^{\phantom a 2} + M_-^2}\right]$](img502.png) |
|||
| (3.97) |
ou seja, neste caso campos magnéticos estáticos não
sofrem o processo de blindagem. Matematicamente, este resultado é
uma consequência de ![]() a um laço. Note que mesmo no caso
bosônico
a um laço. Note que mesmo no caso
bosônico ![]() é nula. Lá, porém, o pólo não
massivo não se desenvolve porque
é nula. Lá, porém, o pólo não
massivo não se desenvolve porque
![]() . Como veremos
na próxima seção, este resultado para o caso fermiônico é
válido em qualquer ordem de perturbação. Pictoricamente,
podemos entendê-lo da seguinte maneira: na
. Como veremos
na próxima seção, este resultado para o caso fermiônico é
válido em qualquer ordem de perturbação. Pictoricamente,
podemos entendê-lo da seguinte maneira: na ![]() o termo de
Chern-Simons não é suficiente para quebrar o comportamento da
massa magnética encontrado na
o termo de
Chern-Simons não é suficiente para quebrar o comportamento da
massa magnética encontrado na ![]() . Já no caso bosônico o
fato da massa magnética não ser nulo pode estar associado com as
soluções tipo vórtice eletricamente carregados existentes na teoria de Higgs abeliana
acoplada com campo de Chern-Simons em
. Já no caso bosônico o
fato da massa magnética não ser nulo pode estar associado com as
soluções tipo vórtice eletricamente carregados existentes na teoria de Higgs abeliana
acoplada com campo de Chern-Simons em ![]() dimensões.
dimensões.