Como foi visto na seção anterior, a massa magnética na ![]() mesmo com a inclusão na teoria de um termo de Chern-Simons, é nula
a um laço. Na análise desenvolvida, este resultado foi uma
consequência de
mesmo com a inclusão na teoria de um termo de Chern-Simons, é nula
a um laço. Na análise desenvolvida, este resultado foi uma
consequência de ![]() no limite estático e é, de certa
forma, reminiscente do resultado encontrado na
no limite estático e é, de certa
forma, reminiscente do resultado encontrado na ![]() . Este
comportamento é surpreendente, uma vez que em
. Este
comportamento é surpreendente, uma vez que em ![]() dimensões o
termo de Chern-Simons assume um papel importante na teoria
fermiônica, modificando intrinsicamente seu carácter
eletromagnético. Mesmo assim, ele não é suficiente para gerar
uma massa magnética ao sistema. Um estudo detalhado desta questão foi
desenvolvido em [27]. Naquele trabalho mostramos que
dimensões o
termo de Chern-Simons assume um papel importante na teoria
fermiônica, modificando intrinsicamente seu carácter
eletromagnético. Mesmo assim, ele não é suficiente para gerar
uma massa magnética ao sistema. Um estudo detalhado desta questão foi
desenvolvido em [27]. Naquele trabalho mostramos que
![]() , através de um cálculo direto a dois laços e de um
prova geral, válida em qualquer ordem de
perturbação. Apresentaremos a seguir tal análise.
, através de um cálculo direto a dois laços e de um
prova geral, válida em qualquer ordem de
perturbação. Apresentaremos a seguir tal análise.
Da decomposição do tensor de polarização,
Eq. (3.59), podemos concluir que, para uma dimensão
![]() qualquer,
qualquer, ![]() pode ser escrito como:
pode ser escrito como:
ou seja, ![]() não depende da estrutura do termo com
quebra de paridade do tensor de polarização e pode ser
determinado diretamente de
não depende da estrutura do termo com
quebra de paridade do tensor de polarização e pode ser
determinado diretamente de ![]() .
.
Indo para o cálculo a um laço podemos expressar ![]() como sendo:
como sendo:
onde os índices ![]() e
e ![]() indicam respectivamente
as aproximações de árvore e um laço. Usando que:
indicam respectivamente
as aproximações de árvore e um laço. Usando que:
| (3.100) |
onde
![]() representa o maior inteiro
menor ou quanto muito igual a
representa o maior inteiro
menor ou quanto muito igual a ![]() , e
, e
![]() , podemos escrever
, podemos escrever
![]() com o uso das Eqs. (3.109) e (3.110) como sendo:
com o uso das Eqs. (3.109) e (3.110) como sendo:
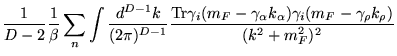 |
|||
![$\displaystyle - \frac{C(D)
e^2}{2(D-2)}\int \frac{d^{D-1} k}{(2 \pi)^{D-1}} \le...
...tial}{\partial w_k}\right] \left[\frac{
\tanh(\frac{\beta w_k}{2})}{w_k}\right]$](img521.png) |
|||
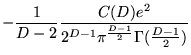 |
|||
![$\displaystyle \int_0^{\infty} dk k^{D-2}\left[(D-1) +
\frac{k^2}{w_k} \frac{\partial}{\partial w_k}\right] \left[\frac{
\tanh(\frac{\beta w_k}{2})}{w_k}\right],$](img523.png) |
(3.101) |
onde
![]() . Considerando somente o termo
dependente da temperatura, temos:
. Considerando somente o termo
dependente da temperatura, temos:
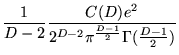 |
|||
![$\displaystyle \int_0^{\infty} dk k^{D-2}\left[(D-1) +
\frac{k^2}{w_k} \frac{\partial}{\partial w_k}\right] \left[\frac{
n_F(w_k)}{w_k}\right],$](img527.png) |
(3.102) |
onde ![]() representa a distribuição de Fermi-Dirac,
ou seja,
representa a distribuição de Fermi-Dirac,
ou seja,
| (3.103) |
Agora, fazendo uma mudança na variável de integração chegamos a:
![$\displaystyle \frac{1}{D-2}\frac{C(D) e^2}{2^{D-2} \pi^{\frac{D-1}{2}}
\Gamma(\...
...\partial
w_k}\left[ (w^2_k - m_F^2)^{\frac{D-1}{2}} \frac{n_F(w_k)}{w_k}\right]$](img530.png) |
|||
| (3.104) |
para ![]() . Este resultado, em geral, é válido
somente para o termo com temperatura finita, que não apresenta
divergência ultravioleta. Em uma dimensão
. Este resultado, em geral, é válido
somente para o termo com temperatura finita, que não apresenta
divergência ultravioleta. Em uma dimensão ![]() qualquer, a
contribuição independente da temperatura não pode ser
incluída na expressão acima, devido a problemas com divergência
ultravioleta. Em
qualquer, a
contribuição independente da temperatura não pode ser
incluída na expressão acima, devido a problemas com divergência
ultravioleta. Em ![]() dimensões, porém, inclusive este termo
pode ser considerado, uma vez que a divergência ultravioleta nele
existente pode ser renormalizada [9]. Em tal situação,
mesmo o termo independente da temperatura se anula.
dimensões, porém, inclusive este termo
pode ser considerado, uma vez que a divergência ultravioleta nele
existente pode ser renormalizada [9]. Em tal situação,
mesmo o termo independente da temperatura se anula.
É de se esperar que um cálculo a dois laços seja mais
complicado, mas lembrando que o anulamento de ![]() a um laço
deu-se devido a uma derivada total do integrando, podemos buscar
este mesmo tipo de estrutura a dois laços. Com esta expectativa,
vamos estudar tal correção. Neste caso, existem dois diagramas
a serem calculados,
a um laço
deu-se devido a uma derivada total do integrando, podemos buscar
este mesmo tipo de estrutura a dois laços. Com esta expectativa,
vamos estudar tal correção. Neste caso, existem dois diagramas
a serem calculados,
![]() e
e
![]() ,
figura (3.4), respectivamente expressos por:
,
figura (3.4), respectivamente expressos por:
| (3.105) |
e
| (3.106) |
onde definimos:
| (3.107) |
e
| (3.108) |
Podemos simplificar estas expressões utilizando a invariância de
calibre da teoria. Assim, definindo a amplitude com quatro fótons
externos a um laço,
![]() ,
como sendo:
,
como sendo:
| (3.109) |
então vale que:
| (3.110) |
devido à invariância de calibre de
![]() . Desta forma temos que:
. Desta forma temos que:
| (3.111) |
Com estas simplificações sendo utilizadas, somamos as duas contribuições ao tensor de polarização a dois laços, finalmente chegando, após algumas manipulações algébricas, a:
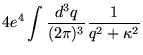 |
|||
![$\displaystyle \int \frac{d^3 k}{(2 \pi)^3} \frac{\partial}{\partial
k_i}\left\{...
...t[q^2 + 4 m_F(\kappa
- m_F)\right]}{(k^2 + m_F^2)^2[(k+q^2)^2 + m_F^2]}\right\}$](img546.png) |
|||
| (3.112) |
ou seja, de maneira análoga ao cálculo a um
laço, chegamos a uma derivada total que se anula na
integração ![]() , incluindo o termo com temperatura nula.
, incluindo o termo com temperatura nula.