Prova Geral

Para estudarmos a generalização dos resultados anteriores para qualquer ordem de perturbação, vamos inicialmente escrever a fórmula geral de $\Pi_1(0)$, utilizando a relação de Schwinger-Dyson, figura (3.5):

$$\Pi_1(0) \equiv \Pi_{ii}(0)$$

$$= \frac{e}{\beta} \sum_n \int\frac{d^2k}{(2 \pi)^2} \mbox{Tr} \gamma_i S(k) \Gamma_i (k,-k,0) S(k),$$ (3.113)

onde $S(k)$ e $\Gamma_i$ são o propagador e a função de vértice completos da teoria, respectivamente. Agora precisamos obter uma relação entre estas duas funções a temperatura finita. Note que no formalismo usual esta relação é dada através da forma diferencial da identidade de Ward [42]. No formalismo de tempo imaginário, entretanto, a generalização desta igualdade não é direta, devido a dificuldades relacionadas com a não analiticidade das amplitudes na origem do plano energia-momento. Na aproximação de árvore sabemos que:

$$\frac{\partial S^{(0)} (p)}{\partial p_{\mu} } = - S^{(0)}(p) \gamma_{\mu} S^{(0)}(p),$$ (3.114)

ou, em outras palavras,

$$\frac{[\partial S^{(0)} (p)]^{-1} }{\partial p_{\mu} } = \gamma_{\mu}.$$ (3.115)

Figura 3.5: Relação de Schwinger-Dyson para a auto-energia do fóton. As linhas internas representam o propagador completo e o círculo, o vértice completo.

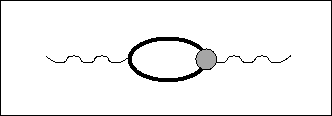Para tentar obter alguma possível informação em ordens superiores, vamos olhar para função de $N$ pontos do fóton a um laço, ou seja,

$$\Gamma_{\mu_1, \mu_2,...,\mu_N} (q_1,q_2,...,q_N) = \int \frac{d^3k}{(2 \pi)^3} \tilde{\Gamma}_{\mu_1, \mu_2,...,\mu_N}(k;q_1,q_2,...,q_N)$$

$$\equiv \frac{1}{\beta} \sum_n \int \frac{d^2k}{(2\pi)^2} \tilde{\Gamma}_{\mu_1, \mu_2,...,\mu_N}(k;q_1,q_2,...,q_N).$$

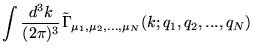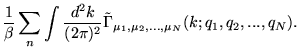Usando a Eq. (3.126), podemos ver que se inserirmos nesta função mais uma linha externa de fóton com índice espacial e tensor energia-momento nulo, então vale que:

$$\Gamma_{i, \mu_1, \mu_2,...,\mu_N} (0;q_1,q_2,...,q_N) = \frac{1}{\beta} \sum_n \int \frac{d^2k}{(2\pi)^2} \tilde{\Gamma}_{i,\mu_1, \mu_2,...,\mu_N}(k;0,q_1,q_2,...,q_N)$$

$$\equiv \frac{1}{\beta} \sum_n \int \frac{d^2k}{(2\pi)^2} \frac{\partial}{\partial k_i}\tilde{\Gamma}_{\mu_1, \mu_2,...,\mu_N}(k;q_1,q_2,...,q_N)$$

$$\equiv 0.$$ (3.116)

Esta é uma espécie de generalização do Teorema de Furry: qualquer laço fermiônico com um fóton externo carregando índice espacial e sem energia nem momento se anula (figura (3.6)).

Figura 3.6: Anulamento dos laços fermiônicos com um dos fótons externos carregando um índice espacial e sem energia nem momento.

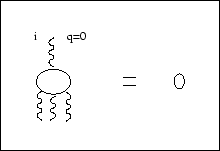Uma consequência direta deste resultado é que, em qualquer ordem temos:

$$\Gamma_i (p,-p,0) = e \frac{\partial S^{-1} (p)}{\partial p_i},$$ (3.117)

ou seja, obtemos para $T \ne 0$ um resultado semelhante à Identidade de Ward no formalismo usual, mas válido somente para os índices espaciais. Esta igualdade é óbvia na aproximação de árvore. Já em uma ordem arbitrária, usando a identidade (3.128), podemos ver que um vértice do tipo $\psi \bar{\psi} A_{\mu}$ com a linha de fóton com índice espacial e sem energia nem momento se anula (figura (3.7)). Com o uso desta propriedade, a atuação da derivada na função de dois pontos completa pode ser obtida ordem a ordem (figura (3.8)), de forma a chegarmos na Eq. (3.129).

Figura 3.7: Anulamento dos vértices conténdo a linha de fóton carregando um índice espacial e sem energia e momento.

Figura 3.8: Atuação da derivada com relação ao momento externo em um diagrama qualquer.

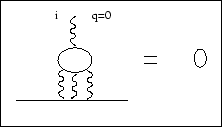Voltando para a expressão de $\Pi_1(0)$, Eq. (3.124), temos que:

$$\Pi_1(0) = \frac{e}{\beta} \sum \int\frac{d^2k}{(2 \pi)^2} \mbox{Tr} \gamma_i S(k) \Gamma_i (k,-k,0) S(k)$$

$$= \frac{e^2}{\beta} \sum \int\frac{d^2k}{(2 \pi)^2} \mbox{Tr} \gamma_i S(k) \frac{\partial S^{-1}(k)}{\partial k_i} S(k)$$

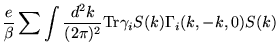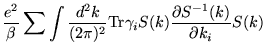$$= - \frac{e^2}{\beta} \sum \int\frac{d^2k}{(2 \pi)^2} \frac{\partial}{\partial k_i} \left[\mbox{Tr} \gamma_i S(k)\right]$$

$$\equiv 0.$$ (3.118)

Vemos da análise acima, que este resultado é geral e válido em qualquer ordem de perturbação.