Higher-Order Filters

Since the first-order filter defined here is linear, one can construct higher-order filters by simply applying it multiple times to a given real function. Consider the first-order filter of range $\varepsilon$ written in terms of the first-order kernel,

$$f_{\varepsilon}^{(1)}(x) = \int_{-\infty}^{\infty}dx'\, K_{\varepsilon}^{(1)}\!\left(x-x'\right) f\!\left(x'\right),$$

where the first-order kernel is given, now in full detail, by the piece-wise description

$$% \renewedcommand{arraystretch}{2.0} \begin{array}{rclcc... ... & \mbox{for} & \left(x-x'\right)<-\varepsilon. \end{array}$$ (2)

Note that, although this is not important for its operation, at the points of discontinuity we define the value of the kernel as the average of the two lateral limits to that point. These are the values to which its Fourier series converges at these points. With this the kernel can also be given by the Fourier representation within $[-\pi ,\pi ]$, if $\varepsilon\leq\pi$,

$$K_{\varepsilon}^{(1)}\!\left(x-x'\right) = \frac{1}{2\pi}... ...\varepsilon)} \right] \cos\!\left[k\left(x-x'\right)\right].$$

Using the representation in terms of an integral operator it is easy to compose two instances of the first-order filter in order to obtain a second-order one, with range $2\varepsilon$,

$$\begin{eqnarray*} f_{2\varepsilon}^{(2)}(x) & = & \int_{-\infty}^{\infty}dx'\... ...K_{2\varepsilon}^{(2)}\!\left(x-x''\right) f\!\left(x''\right), \end{eqnarray*}$$

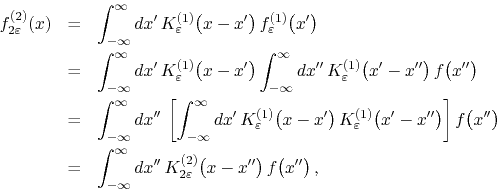
where the second-order kernel with range $2\varepsilon$ is given by the application of the first-order filter to the first-order kernel,

$$K_{2\varepsilon}^{(2)}\!\left(x-x''\right) = \int_{-\inft... ...\left(x-x'\right) K_{\varepsilon}^{(1)}\!\left(x'-x''\right).$$

It is not difficult to show by direct calculation of the integral that this second-order kernel is given by the piece-wise description

$$% \renewedcommand{arraystretch}{2.0} \begin{array}{rclcc... ...\mbox{for} & \left(x-x'\right)\leq-2\varepsilon, \end{array}$$

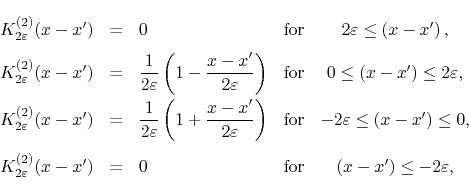
which makes its range explicit. It is also given by the Fourier representation within $[-\pi ,\pi ]$, so long as $\varepsilon\leq\pi/2$,

$$K_{2\varepsilon}^{(2)}\!\left(x-x'\right) = \frac{1}{2\pi... ...epsilon)} \right]^{2} \cos\!\left[k\left(x-x'\right)\right].$$

The calculation of the coefficients of this series is just as straightforward as the one for the first-order kernel. Due to the factor of $k^{2}$ in the denominator, this series is absolutely and uniformly convergent over the whole periodic interval. The result shown above also follows from the property of the first-order filter regarding its action on Fourier expansions, listed as item 12 on page , which is demonstrated in Section A.12 of Appendix A. Note that, according to the property listed as item 9 on page , which is demonstrated in Section A.9 of Appendix A, the first-order filter does not change the definite integral of the compact-support function it is applied on, and since $K_{\varepsilon}^{(1)}\!\left(x-x'\right)$ is an even function with unit integral and compact support, it follows that $K_{2\varepsilon}^{(2)}\!\left(x-x'\right)$ is also an even function with unit integral and compact support, since it is given by the first-order kernel $K_{\varepsilon}^{(1)}\!\left(x-x'\right)$ filtered by the first-order filter.

The range of the first-order filter, within which the functions are significantly changed by it, is given by $\varepsilon$, and if one just applies the filter twice, as we did above, that range doubles do $2\varepsilon$. However, one may compensate for this by simply applying twice the first-order filter with parameter $\varepsilon/2$, thus resulting in a second-order filter with range $\varepsilon$. In this way one may define higher-order filters while keeping the relation of the range to the relevant physical scale constant. For example, we have the second-order filter with range $\varepsilon$ defined by the kernel

$$K_{\varepsilon}^{(2)}\!\left(x-x''\right) = \int_{-\infty... ...eft(x-x'\right) K_{\varepsilon/2}^{(1)}\!\left(x'-x''\right).$$

It is immediate to obtain the piece-wise description of this kernel from that of $K_{2\varepsilon}^{(2)}\!\left(x-x'\right)$,

$$% \renewedcommand{arraystretch}{2.0} \begin{array}{rclcc... ... \mbox{for} & \left(x-x'\right)\leq-\varepsilon. \end{array}$$

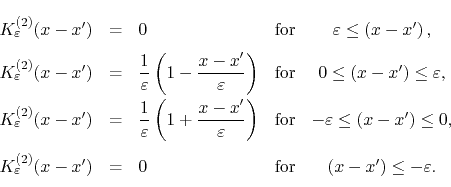
It is equally immediate to obtain the Fourier representation of this kernel within $[-\pi ,\pi ]$, which so long as $\varepsilon\leq\pi$ is given by

$$K_{\varepsilon}^{(2)}\!\left(x-x'\right) = \frac{1}{2\pi}... ...silon/2)} \right]^{2} \cos\!\left[k\left(x-x'\right)\right].$$

This procedure can be iterated $N$ times to produce an order-$N$ filter. One can verify on a case-by-case fashion that such a filter is given by a piece-wise kernel formed of polynomials of order $N-1$ on $N$ equal-length intervals between $-N\varepsilon$ and $N\varepsilon$, each interval of length $2\varepsilon$, with the polynomials connected to each other in a maximally smooth way. Since the filter of order $N$ is obtained by the application of the first-order filter to the result of the filter of order $N-1$, it follows that the kernel of order $N$ is the kernel of order $N-1$ filtered by the first-order filter. Due to this, and recalling again the property of the first-order filter regarding its action on Fourier expansions, listed as item 12 on page , the Fourier representation of the order-$N$ kernel of range $N\varepsilon$ can be easily written explicitly,

$$K_{N\varepsilon}^{(N)}\!\left(x-x'\right) = \frac{1}{2\pi... ...epsilon)} \right]^{N} \cos\!\left[k\left(x-x'\right)\right],$$

so long as $\varepsilon\leq\pi/N$. This expression can be extended to the case $N=0$, which corresponds to an order-zero filter that has the Dirac delta ``function'' as its kernel, since the delta ``function'' can be represented by the divergent series

$$\begin{eqnarray*} \delta\!\left(x-x'\right) & = & K_{0}^{(0)}\!\left(x-x'\rig... ...pi} \sum_{k=1}^{\infty} \cos\!\left[k\left(x-x'\right)\right], \end{eqnarray*}$$

as is discussed in detail in [2]. We see in this way that the first-order kernel $K_{\varepsilon}^{(1)}\!\left(x-x'\right)$ can in fact be obtained by the application of the first-order filter to the delta ``function'', as is discussed in more detail in Section A.5 of Appendix A.

In this construction the range of the filter increases with $N$, so that one cannot iterate in this way indefinitely inside the periodic interval without the range eventually becoming larger than the length of the interval. However, we may keep the overall range constant at the value $\varepsilon$ by decreasing the range of the first-order filter at each level of iteration, that is, by iterating $N$ times the first-order filter of range $\varepsilon/N$. If we simply exchange $\varepsilon$ for $\varepsilon/N$ in the expression above we get the order-$N$ kernel with range $\varepsilon$, written in quite a simple way in terms of its Fourier expansion,

$$K_{\varepsilon}^{(N)}\!\left(x-x'\right) = \frac{1}{2\pi}... ...silon/N)} \right]^{N} \cos\!\left[k\left(x-x'\right)\right],$$

Figure 1: The kernels of the first few lower-order filters with constant range $\varepsilon$, obtained via the use of their Fourier series, for $N=1,\ldots,8$ and $\varepsilon =0.5$, plotted as functions of $\left (x-x'\right )$ over their common support within the periodic interval $[-\pi ,\pi ]$.

so long as $\varepsilon\leq\pi$. Since the range is now constant, one can consider iterations of any order $N$, without any upper bound, even within the periodic interval. Note that this series converges ever faster as $N$ increases. Note also that it can be differentiated $N-2$ times still resulting in a absolutely and uniformly convergent series, and $N-1$ times still resulting in a point-wise convergent series. This is a reflection of the fact that the polynomials that compose the kernel are connected to each other in the maximally smooth way. Apart from the case of the order-zero kernel, which has a divergent Fourier series, the series for $K_{\varepsilon}^{(1)}\!\left(x-x'\right)$ is the only one which is not absolutely or uniformly convergent, although it is point-wise convergent. For $N\geq 2$ all the kernel series are absolutely and uniformly convergent to functions of differentiability class $C^{N-2}$ everywhere. The kernels of the filters of the first few orders, with constant range $\varepsilon$, are shown in Figure 1. The program used to plot this graph is available online [4].

As we saw above, the order-$N$ kernels are themselves a good example of the smoothing action of the filters. As we verified in that case, the use of higher-order filters will have the effect of introducing more powers of $k$ in the denominators of the Fourier coefficients $\alpha_{k}$ and $\beta_{k}$, and hence of making the Fourier series converge faster and to smoother functions. This will then enable one to take a certain number of term-wise derivatives of the series, as may be required by the applications involved. Besides, all this can be done within a small constant length scale determined by $\varepsilon$, leaving essentially untouched the description of the physics at the larger scales.