Action on Dirac's Delta ``Function''

Let us assume that we have the ``function'' $f(x)=\delta(x-x_{0})$. Since this is an integrable object, we may calculate the corresponding filtered function, which as we shall see is in fact an actual function. The function $f_{\varepsilon}(x)$ that corresponds to $f(x)$ through the first-order filter of range $\varepsilon$ is, by definition,

$$f_{\varepsilon}(x) = \frac{1}{2\varepsilon} \int_{x-\varepsilon}^{x+\varepsilon}dx'\,\delta(x'-x_{0}).$$

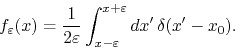
By the properties of the delta ``function'', this integral will be equal to $1$ if the point $x_{0}$ is within the integration interval, and $0$ if it is outside. The point $x_{0}$ can only be within the integration interval if the distance between $x$ and $x_{0}$ is smaller than $\varepsilon$, that is, if $\vert x-x_{0}\vert<\varepsilon$. Therefore we have for the resulting function the piece-wise description

$$% \renewedcommand{arraystretch}{2.1} \begin{array}{rclcl... ...) & = & 0 & \mbox{if} & (x_{0}+\varepsilon)<x. \end{array}$$

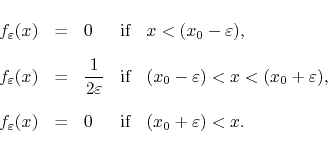
This is a rectangular pulse centered at $x_{0}$, with height $1/(2\varepsilon)$ and width $(2\varepsilon)$, having therefore unit area. Note that this is, in fact, the first-order kernel itself, that is

$$f_{\varepsilon}(x) = K_{\varepsilon}^{(1)}(x-x_{0}).$$

This one-parameter family of functions is one that is commonly used for the very definition the Dirac delta ``function'' in the limit $\varepsilon\to 0$, and therefore we have that

$$\lim_{\varepsilon\to 0}K_{\varepsilon}^{(1)}(x-x_{0}) = \delta(x-x_{0}).$$

Looking at the filter as an operator in some larger space of integrable objects, this means that it becomes the identity in the $\varepsilon\to 0$ limit, in so far as delta ``functions'' are concerned. Note that the delta ``function'' can also be understood as the kernel of an order-zero filter,

$$f_{0}^{(0)}(x) = \int_{-\infty}^{\infty}dx'\, \delta\!\left(x-x'\right)f\!\left(x'\right).$$

This filter is the identity where $f(x)$ is continuous, so that typically it is the identity almost everywhere. Note also that, as a particular case of this expression, we may conclude that the first-order kernel is the result of the application of the first-order filter to the delta ``functions'',

$$K_{\varepsilon}^{(1)}\!\left(x-x''\right) = \int_{-\infty... ...psilon}^{(1)}\!\left(x'-x''\right) \delta\!\left(x-x'\right),$$

which holds everywhere so long as the first-order kernel is defined as we did in Equation (2) and so long as we use the average of the two lateral limits as the value given by the integral of the delta ``function'' at a point of discontinuity of the function involved.