Continuity of Filtered Functions

Let us show that for any integrable function $f(x)$ the filtered function $f_{\varepsilon}(x)$ is continuous. We simply calculate the filtered function at $x$ and $x+\Delta x$ and then make $\Delta x\to 0$. The variation of $f_{\varepsilon}(x)$ is given by

$$\begin{eqnarray*} \Delta f_{\varepsilon}(x) & = & f_{\varepsilon}(x+\Delta x)... ... \int_{x-\varepsilon}^{x+\varepsilon}dx'\, f\!\left(x'\right). \end{eqnarray*}$$

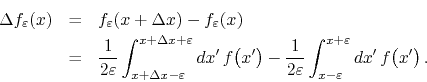
For any given value of $\varepsilon$, in the $\Delta x\to 0$ limit we will eventually have $\Delta x\ll \varepsilon$, and then the domains of the two integrals overlap in most of their extent, which we can see decomposing the integrals as

$$\begin{eqnarray*} \Delta f_{\varepsilon}(x) & = & \frac{1}{2\varepsilon} \in... ...)}^{(x-\varepsilon)+\Delta x}dx'\, f\!\left(x'\right) \right]. \end{eqnarray*}$$

We have here two integrals over intervals of length $\Delta x$. In the $\Delta x\to 0$ limit we have integrals over zero-measure domains, and since the function $f(x)$ is integrable, the result is zero,

$$\lim_{\Delta x\to 0} \Delta f_{\varepsilon}(x) = 0,$$

regardless of the sign of $\Delta x$, which establishes that $f_{\varepsilon}(x)$ is continuous.