Differentiability of Filtered Functions

Let us show that for any continuous function $f(x)$ the filtered function $f_{\varepsilon}(x)$ is differentiable. We simply calculate the filtered function $f_{\varepsilon}(x)$ at $x$ and $x+\Delta x$, then calculate its variation $\Delta f_{\varepsilon}(x)$, divide by $\Delta x$ and finally make $\Delta x\to 0$. The finite-difference ratio is given by

$$\begin{eqnarray*} \frac{\Delta f_{\varepsilon}(x)}{\Delta x} & = & \frac{f_{\... ... \int_{x-\varepsilon}^{x+\varepsilon}dx'\, f\!\left(x'\right). \end{eqnarray*}$$

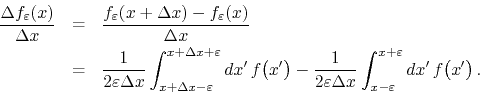
For any given value of $\varepsilon$, in the $\Delta x\to 0$ limit we will eventually have $\Delta x\ll \varepsilon$, and then the domains of the two integrals overlap in most of their extent, which we can see decomposing the integrals as

$$\begin{eqnarray*} \frac{\Delta f_{\varepsilon}(x)}{\Delta x} & = & \frac{1}{2... ...)}^{(x-\varepsilon)+\Delta x}dx'\, f\!\left(x'\right) \right]. \end{eqnarray*}$$

We have here two integrals over intervals of length $\Delta x$, divided by $\Delta x$. These normalized integrals give therefore the average values of $f(x)$ around the points $x+\varepsilon$ and $x-\varepsilon$. Since the function $f(x)$ is integrable these average values are finite, and since it is continuous, the average value tends to the value of the function when $\Delta x\to 0$, so that we get

$$\lim_{\Delta x\to 0} \frac{\Delta f_{\varepsilon}(x)}{\Del... ...n\right) - f\!\left(x-\varepsilon\right) } {2\varepsilon}.$$

This is true both for positive and negative values of $\Delta x$, and the limit manifestly exists and has the value shown, which is independent of the sign of $\Delta x$. Therefore, this establishes that $f_{\varepsilon}(x)$ is differentiable.