Next: Differentiability of Filtered Functions Up: Appendix: Properties of the Previous: Invariance of Linear Functions
Let us determine the action of the filter on a function which is a simple
power on the real line. If ![]() then we have
then we have
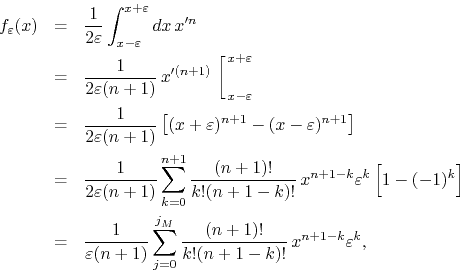
where ![]() and
and ![]() if
if ![]() is even, while
is even, while ![]() if
if
![]() is odd. We have therefore
is odd. We have therefore
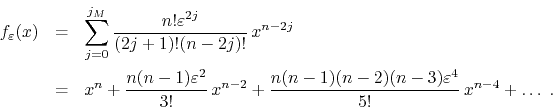
We see therefore that the filter preserves the original power, and that
all other terms generated are of lower order and are damped by factors of
![]() . It follows that the filter will reproduce any order-
. It follows that the filter will reproduce any order-![]() polynomial, adding to it a lower-order polynomial, of order
polynomial, adding to it a lower-order polynomial, of order ![]() , with
all coefficients damped by powers of
, with
all coefficients damped by powers of
![]() . Therefore, in the
. Therefore, in the
![]() limit the filter reduces to the identity, in so far as
polynomials are concerned.
limit the filter reduces to the identity, in so far as
polynomials are concerned.