Invariance of Linear Functions

Let us show that if $f(x)$ is a linear function on the real line, then $f_{\varepsilon}(x)=f(x)$. It suffices to simply calculate $f_{\varepsilon}(x)$. We have $f(x)=a+bx$, so that

$$\begin{eqnarray*} f_{\varepsilon}(x) & = & \frac{1}{2\varepsilon} \int_{x-\v... ...bx\varepsilon \right) \\ & = & a + 2bx \\ & = & f(x). \end{eqnarray*}$$

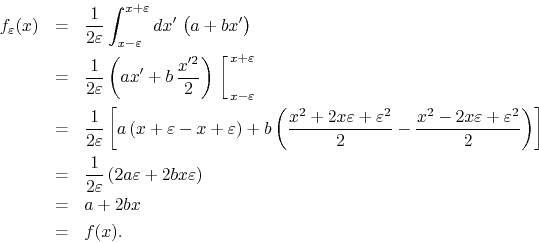
Note that if a function is defined in a piece-wise fashion, in any section where it is linear the filter is the identity at all points $x$ where the interval $(x-\varepsilon,x+\varepsilon)$ fits completely inside the section. Therefore, in the $\varepsilon\to 0$ limit the filter becomes the identity in the whole interior of such a section.