Next: Points of Discontinuity Up: Appendix: Properties of the Previous: Action on Dirac's Delta
Let us show that in the
![]() limit the filter reduces to an
almost-identity operation, in the sense that it reproduces in the output
function
limit the filter reduces to an
almost-identity operation, in the sense that it reproduces in the output
function
![]() the input function
the input function ![]() almost everywhere.
If we consider the well-known relation mentioned in the previous section
as a possible definition of the Dirac delta ``function'', as the
almost everywhere.
If we consider the well-known relation mentioned in the previous section
as a possible definition of the Dirac delta ``function'', as the
![]() limit of the first-order kernel
limit of the first-order kernel
![]() , it becomes clear that we have,
for an arbitrary integrable function
, it becomes clear that we have,
for an arbitrary integrable function ![]()
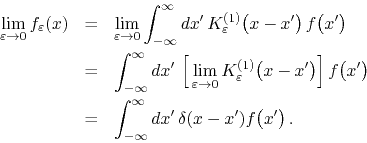
According to the properties of the delta ``function'', this integral
returns the value ![]() at every point where this function is continuous.
We therefore have
at every point where this function is continuous.
We therefore have
at every point where ![]() is continuous. Since this may fail at a finite
(or at least zero-measure) set of points where
is continuous. Since this may fail at a finite
(or at least zero-measure) set of points where ![]() is discontinuous, we
say that in the
is discontinuous, we
say that in the
![]() limit the first-order filter reduces to
the identity almost everywhere. We may also say that the filter becomes an
almost-identity operation in the limit. What happens at the points of
discontinuity of
limit the first-order filter reduces to
the identity almost everywhere. We may also say that the filter becomes an
almost-identity operation in the limit. What happens at the points of
discontinuity of ![]() is discussed in the next section.
is discussed in the next section.