Next: Points of Non-Differentiability Up: Appendix: Properties of the Previous: Reduction to the Identity
Let us show that in the
![]() limit the function
limit the function
![]() essentially reproduces the original function
essentially reproduces the original function
![]() . Stating it more precisely, we will show that, if the function
. Stating it more precisely, we will show that, if the function
![]() has an isolated point of discontinuity at
has an isolated point of discontinuity at ![]() , then in the
, then in the
![]() limit
limit
![]() tends to the average of
the two lateral limits of
tends to the average of
the two lateral limits of ![]() to the point
to the point ![]() , that is,
, that is,
where
regardless of the value that ![]() assumes at
assumes at ![]() . In particular, if
. In particular, if
![]() is continuous at
is continuous at ![]() , then
, then
![]() and hence
and hence
![]() tends to
tends to ![]() in the limit, thus
reproducing the original function at that point.
in the limit, thus
reproducing the original function at that point.
Here is the proof: if ![]() has an isolated point of discontinuity at
has an isolated point of discontinuity at
![]() , then there are two neighborhoods of
, then there are two neighborhoods of ![]() , one to the left and
another one to the right, where
, one to the left and
another one to the right, where ![]() is continuous. For sufficiently
small
is continuous. For sufficiently
small ![]() , the interval of integration will fit into this
combined neighborhood, so that the only point of discontinuity within it
will be
, the interval of integration will fit into this
combined neighborhood, so that the only point of discontinuity within it
will be ![]() . Let us consider then the value of
. Let us consider then the value of
![]() , as given by the definition,
, as given by the definition,
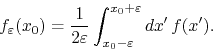
We may separate this integral in two, one in the left neighborhood and another one in the right neighborhood,
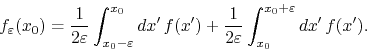
Since the function ![]() is integrable, the integrals converge to
is integrable, the integrals converge to
![]() times the average value of the function over each
sub-interval, so that we have
times the average value of the function over each
sub-interval, so that we have
Finally, since the function ![]() is continuous in each sub-interval, in
the
is continuous in each sub-interval, in
the
![]() limit each average value converges to the
corresponding lateral limit of
limit each average value converges to the
corresponding lateral limit of ![]() , so that we have
, so that we have
where
This establishes the result. As a consequence of this, if ![]() is
continuous at
is
continuous at ![]() , then
, then
![]() , and
therefore we have
, and
therefore we have
We therefore conclude that in the
![]() limit the filtered
function
limit the filtered
function
![]() reproduces the original function
reproduces the original function ![]() where it is continuous. There may be isolated points of discontinuity
where this fails, and therefore we say that in the
where it is continuous. There may be isolated points of discontinuity
where this fails, and therefore we say that in the
![]() limit the filtered function
limit the filtered function
![]() reproduces the original
function
reproduces the original
function ![]() almost everywhere.
almost everywhere.