Next: Invariance of Definite Integrals Up: Appendix: Properties of the Previous: Points of Discontinuity
Let us show that in the
![]() limit the derivative of the
function
limit the derivative of the
function
![]() essentially reproduces the derivative of the
original function
essentially reproduces the derivative of the
original function ![]() . Stating it more precisely, we will show that, if
the function
. Stating it more precisely, we will show that, if
the function ![]() is continuous but has an isolated point of
non-differentiability at
is continuous but has an isolated point of
non-differentiability at ![]() , then in the
, then in the
![]() limit the
derivative of
limit the
derivative of
![]() tends to the average of the two
lateral limits of the derivative of
tends to the average of the two
lateral limits of the derivative of ![]() to the point
to the point ![]() , that is,
, that is,
where
regardless of any value that may be artificially given to the derivative
of ![]() at
at ![]() . In particular, if
. In particular, if ![]() is differentiable at
is differentiable at
![]() , then
, then ![]() and
and ![]() are both equal to the
derivative of
are both equal to the
derivative of ![]() at
at ![]() , and hence the derivative of
, and hence the derivative of
![]() tends to the derivative of
tends to the derivative of ![]() at
at ![]() in the
limit, thus reproducing the derivative of the original function at that
point.
in the
limit, thus reproducing the derivative of the original function at that
point.
Here is the proof: if ![]() is continuous at
is continuous at ![]() and has an isolated
point of discontinuity there, then there are two neighborhoods of
and has an isolated
point of discontinuity there, then there are two neighborhoods of ![]() ,
one to the left and another one to the right, where
,
one to the left and another one to the right, where ![]() is continuous
and differentiable. According to the results of Section A.3
of this Appendix, since
is continuous
and differentiable. According to the results of Section A.3
of this Appendix, since ![]() is continuous at and around
is continuous at and around ![]() ,
,
![]() is differentiable and its derivative at
is differentiable and its derivative at ![]() is
given by
is
given by
However, since ![]() is not differentiable at
is not differentiable at ![]() , the
, the
![]() limit of the right-hand side of this equation does not
give us any definite results. We may however separate this expression in
two, each one making reference to only one of the two neighborhoods,
limit of the right-hand side of this equation does not
give us any definite results. We may however separate this expression in
two, each one making reference to only one of the two neighborhoods,
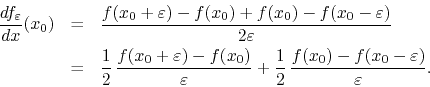
It is now clear that, since ![]() is differentiable in the two lateral
neighborhoods, in the
is differentiable in the two lateral
neighborhoods, in the
![]() limit the two terms in the
right-hand side of this equation converge respectively to the right and
left derivatives of
limit the two terms in the
right-hand side of this equation converge respectively to the right and
left derivatives of ![]() at
at ![]() . We therefore have
. We therefore have
where
This establishes the result. In particular, if ![]() is differentiable at
is differentiable at
![]() , then
, then ![]() and
and ![]() are both equal to the
derivative of
are both equal to the
derivative of ![]() at
at ![]() , and therefore we have for the derivative
of
, and therefore we have for the derivative
of
![]() at
at ![]()
thus reproducing the derivative of the original function at that point.