Next: Periodicity of Filtered Functions Up: Appendix: Properties of the Previous: Points of Non-Differentiability
Let us determine the effect of the filter on the definite integral of a
function ![]() with compact support on the real line. We may write the
integral as
with compact support on the real line. We may write the
integral as
where the integrand is non-zero only inside a closed interval. The
integral of the filtered function
![]() has support on
another closed interval, that of
has support on
another closed interval, that of ![]() increased by
increased by ![]() in each
direction, and is similarly given by
in each
direction, and is similarly given by
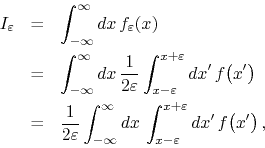
where we used the definition of
![]() in terms of
in terms of ![]() .
We now make the change of variables
.
We now make the change of variables ![]() on the inner integral,
implying
on the inner integral,
implying ![]() and
and ![]() , leading to
, leading to
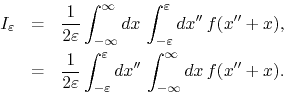
Since the integral on ![]() is over the whole real line, we may now change
variables on it without changing the integration limits, using
is over the whole real line, we may now change
variables on it without changing the integration limits, using ![]() ,
with
,
with ![]() and
and ![]() , and thus obtaining
, and thus obtaining
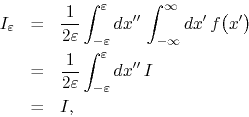
were we recognized the form of the integral ![]() . In this way we show that
. In this way we show that
![]() , that is, the filter does not change the definite
integral at all. Another way to state this is to say that the filter does
not change the average value of
, that is, the filter does not change the definite
integral at all. Another way to state this is to say that the filter does
not change the average value of ![]() over the common support of
over the common support of ![]() and
and
![]() .
.