Next: Invariance of Averages Over Up: Appendix: Properties of the Previous: Invariance of Definite Integrals
Let us show that if ![]() is a periodic function, with a period that we
choose arbitrarily to be
is a periodic function, with a period that we
choose arbitrarily to be ![]() , then
, then
![]() is also
periodic, with the same period. It suffices to simply calculate
is also
periodic, with the same period. It suffices to simply calculate
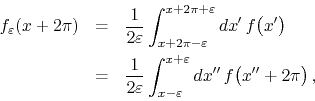
where we changed variables to ![]() , so that
, so that ![]() . Since
. Since
![]() is periodic with period
is periodic with period ![]() , we now have
, we now have
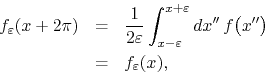
so that we may conclude that
![]() is periodic with period
is periodic with period
![]() .
.