Next: Completeness of the Set Up: Appendix: Properties of the Previous: Invariance of Averages Over
Let us determine the effect of the filter on the Fourier coefficients for
![]() . We start with the Fourier coefficients of
. We start with the Fourier coefficients of ![]() , which are given
by
, which are given
by
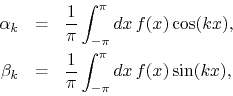
where we arbitrarily chose ![]() as the periodic interval. The
Fourier coefficients of
as the periodic interval. The
Fourier coefficients of
![]() are similarly given by
are similarly given by
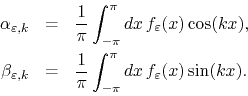
Let us work out only the first case, since the work for the second one in
essentially identical. Using the definition of
![]() in
terms of
in
terms of ![]() we have
we have
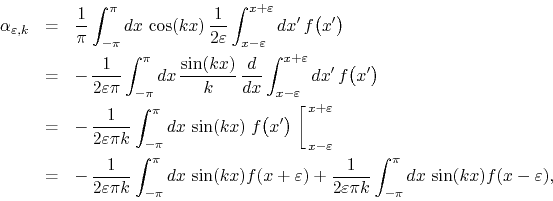
where we integrated by parts and where there is no integrated term due to
the periodicity of the integrand on the domain. We now change variables in
each integral, using
![]() , in order to obtain
, in order to obtain
![\begin{eqnarray*}
\alpha_{\varepsilon,k}
& = &
-\,
\frac{1}{2\varepsilon\pi ...
...ft[
\sin(kx'+k\varepsilon)
-
\sin(kx'-k\varepsilon)
\right],
\end{eqnarray*}](img159.png)
where the integration limits did not change in the transformations of variables due to the periodicity of the integrand on the domain. We are left with
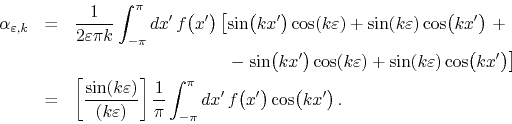
Since we recover in this way the expression of the Fourier coefficients
![]() of
of ![]() , we get
, we get
and repeating the calculation for the other coefficients one gets
Once again we see the sinc function of the variable
![]() appearing here. Since
appearing here. Since
![]() is a limited function, in terms
of the asymptotic behavior of the coefficients, for large values of
is a limited function, in terms
of the asymptotic behavior of the coefficients, for large values of ![]() ,
the net effect of the filter is to add a factor of
,
the net effect of the filter is to add a factor of ![]() to the denominator.
to the denominator.